Упругость и гиперупругость урогенитальных тканей человека и животных

Рис. 1. Кривые напряжения – деформации фиброзной капсулы почки у лиц в возрасте от 10 до 39 лет (экспериментальная и расчетная (функция genfit Mathcad 13))

Таблица 1. Деформационные свойства фиброзной капсулы человека

Рис. 2. Зависимость модуля Юнга фиброзной капсулы почки от деформации у лиц в возрасте от 10 до 39 лет (получена с помощью функции genfit Mathcad 13)

Рис. 3. Кривые зависимостей: опытной σ(λ) и Муни – Ривлина g(t) (получены с помощью функции linfit Mathcad 13) для соединительнотканной капсулы почки

Рис. 4. Кривые напряжения – деформации почечной паренхимы у лиц в возрасте от 10 до 19 лет (экспериментальная и расчетная (функция genfit Mathcad 13))

Таблица 2. Деформационные свойства паренхимы почки человека

Таблица 3. Деформационные свойства мочеточника человека

Рис. 5. Кривые напряжения – деформации мочеточника у лиц в возрасте от 10 до 29 лет (экспериментальные и расчетные с помощью функции genfit Mathcad 13) в продольном (l) и поперечном (t) направлениях

Таблица 4. Деформационные свойства мочевого пузыря человека

Рис. 6. Кривые напряжения – деформации тела (b – body) и треугольника (t – trigone) мочевого пузыря пациентов в возрасте от 10 до 29 лет (экспериментальные и расчетные с помощью функции genfit Mathcad 13)

Рис. 7. Кривые напряжения – деформации для уретры свиноматок

Рис. 8. Реологическая KVFD-модель с неньютоновским вязким элементом (η, α)

Таблица 5. Параметры модели KVFD и коэффициент корреляции r2 расчетных данных с опытными данными

Рис. 9. Модули Юнга двух типов тканей предстательной железы, построенные в зависимости от частоты, и положительная связь между жесткостью тканей и долей рака (0 и 90%) [по 12]

Рис. 10. Жесткость тканей (модуль Юнга) |E*| в сравнении с долей рака в исследованных образцах. Горизонтальная линия разделяет значения жесткости раковых и нормальных тканей. 150 Гц

Таблица 6. Модули упругости тканей в нормальной и измененной ткани предстательной железы при различных частотах и уровнях предкомпрессионной деформации 2 и 4%

Рис. 11. Усредненный модуль Юнга тканей предстательной железы (кПа), полученный при  различных скоростях деформации (0,1; 1,0 и 4,0 Гц) и степени предварительной компрессии (2 и 4%)

Таблица 7. Значения жесткости тканей (модуль Юнга) левого кавернозного тела и белочной оболочки у пациентов с эректильной дисфункцией (ЭД) и в норме (группа контроля) при различной степени (1–4) эректильной твердости по шкале EHS, Mean ± SD

Рис. 12. Модуль Юнга кавернозного тела и белочной оболочки у пациентов с эректильной дисфункцией (ЭД) и в норме (группа контроля) при различной степени эректильной твердости EHS

Рис. 13. Сравнение значений Emean, Emax, Emin и SD тканей нормального яичка и яичка с перекрутом в пограничной (А) и центральной (Б) областях

Рис. 14. Кривые напряжения – деформации матки крольчих. Продольное направление (экспериментальная и расчетная (функция genfit Mathcad 13))

Рис. 15. Значения модуля Юнга матки небеременных женщин в различных локациях (А) и коэффициента Пуассона слоев матки (Б)

Рис. 16. Значения модулей упругости влагалища, шейки матки, тела матки, маточно-крестцовой связки (МКС), кардинальной связки (КС) и круглой связки (КрС), определенные методом наноиндентирования

Рис. 17. Кривые напряжения – деформации стенки влагалища крольчих (экспериментальные и расчетные (функция genfit Mathcad 13)) в продольном (l) и поперечном (t) направлениях

Рис. 18. Эластичность (модуль Юнга) передней стенки влагалища в его апикальной (А) и средней (Б) части [по 45]

Рис. 19. Типичные кривые напряжения – деформации для вагинальной ткани у рожавших, девственных и беременных овец

Рис. 20. Биомеханические свойства вагинальной стенки овец: А – модуль Юнга; Б – предел прочности; В – остаточная деформация; Г – деформация при разрыве девственных, рожавших и беременных особей переднего отдела (голубые столбики) и заднего отдела (желтые

Рис. 21. Box and whiskers значений эффективного модуля Юнга, полученные с помощью наноиндентирования. Логарифмическая шкала вертикальной оси значений lg E, кПа

Рис. 22. Средние модули упругости тканей яичников при эндометриозе, муцинозной цистаденоме, серозной цистаденоме, зрелой тератоме

Таблица 8. Модуль упругости ткани в нормальной ткани молочной железы при различных частотах и уровнях предкомпрессионной деформации 5 и 20%

Рис. 23. Усредненный модуль Юнга тканей молочной железы (кПа), полученный при различных скоростях деформации (0,1; 1,0 и 4,0 Гц) и степени предварительной компрессии (5 и 20%)

Рис. 24. Кривые напряжения – деформации пуповины на 10-м месяце беременности (экспериментальная и расчетная (функция genfit Mathcad 13))

Таблица 9. Упругие и гиперупругие свойства урогенитальных тканей

Рис. 25. Упругие свойства урогенитальных тканей по данным анализа кривых σ = σ(ε): А – линейчатая гистограмма, Б – ‘box and whiskers’

Введение

Проблемы контроля мочевого пузыря затрагивают как мужскую, так и женскую популяцию, и их диапазон весьма широк – от гиперактивного мочевого пузыря и недержания мочи до непроходимости мочевыводящих путей и рака [1]. Подобными расстройствами страдает свыше 200 млн человек во всем мире. Разработка более совершенных и биосовместимых конструкций имплантатов, применяемых в системах контроля для лечения пациентов с недержанием мочи, и искусственных сфинктеров, а также вопросы коррекции пролапса тазовых органов женщин, эректильной дисфункции у мужчин [2] и иные урологические/гинекологические проблемы требуют знаний, касающихся механических свойств урогенитальных тканей.

Почти все биологические ткани (кроме костей скелета, эмали и дентина зубов и др.) характеризуются относительно низким модулем упругости и высоким объемным модулем, а их коэффициент Пуассона немного меньше 0,5. Эти мягкие ткани организма с большими упругими деформациями и небольшим изменением объема (практически несжимаемые материалы) при деформации часто называются гиперупругими материалами. Поведение гиперупругих материалов, называемых также эластомерами, с точки зрения механики деформируемого тела описывается нелинейными законами связи напряжения – деформации. То есть в отличие от линейно-упругих материалов кривая напряжения – деформации гипер­упругого материала не является линейной, а классический закон Гука не выполняется. Для описания деформационных свойств гиперупругих материалов предложены многочисленные реологические модели (в частности, Муни – Ривлина, Нео – Гука, Ривлина, Огдена), а выбор и установление параметров моделей, определяющих соотношения для гиперупругих материалов, представляют также актуальную задачу биомеханики [3].

Материал и методы

На первом этапе известные, но не утратившие актуальности экспериментальные кривые σ–ε были оцифрованы с помощью программы GetData Graph Digitizer. Далее данные были экспортированы в пакет программ для математических вычислений Mathcad 13. Полученные массивы были описаны аналитически экспоненциальными зависимостями вида σ = α(e^βε-1), где коэффициенты α и β находили с помощью функции genfit. Функция genfit возвращает вектор, содержащий n параметров, которые обеспечивают наилучшее приближение данных из ε и σ функцией σ(ε). Этот способ аппроксимации оказался эффективен и показал высокую точность. Затем упругие модули E(ε) определяли дифференцированием соответствующих регрессионных зависимостей E(ε) = dσ(ε) / dε = σ'ε.

Кроме того, рассчитывали константы двухпараметрической и достаточно простой модели Муни – Ривлина биологических тканей на основании опытных кривых по результатам механических испытаний на растяжение. Как известно, поведение гиперупругих материалов при растяжении с точки зрения современной механики деформируемых тел может быть описано нелинейной функцией [4]:

  , (1) 

 где σ – условное напряжение,  C₁₀ и C₀₁ – материальные константы (константы материала). C₁₀ и C₀₁ определяют потенциал деформации:

  . (2)

 I₁ и I₂ – инварианты тензора деформаций, равные

   и   , значения λ_i = ε_i + 1 –  главные компоненты тензора (i = 1, 2, 3). Уравнение (1) является разновидностью 2-параметрического феноменологического уравнения Муни – Ривлина. Анализ проводили в системе компьютерной алгебры Mathcad 13 с помощью встроенной в пакет функции linfit. Как выяснилось, модель Муни – Ривлина с найденными коэффициентами C₁₀ и C₀₁ весьма удовлетворительно описывает биомеханическое поведение урогенитальных тканей, установленное экспериментальным путем.

Часть 1. Мочевыделительная система

Почка

Фиброзная капсула. I. Asami (1961) [5] исследовал деформационные свойства фиброзной (соединительнотканой) капсулы у 67 пациентов.

Фиброзная капсула (capsula fibrosa) – тонкая, но очень прочная оболочка. Она окружает непосредственно саму ткань почки снаружи. Эта оболочка для почки служит прочным футляром, предохраняющим орган от разрывов.

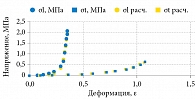
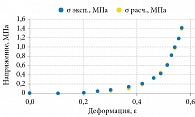
Результаты исследований пациентов в возрасте от 10 до 39 лет представлены на рис. 1. Этап начального удлинения соответствовал около 25% предела прочности капсулы, а само начальное удлинение составляло около трех четвертей предела деформации (табл. 1) [5]. При тех же напряжениях удлинение является наибольшим в 10 лет и уменьшается с возрастом.

Мы связываем такое деформационное поведение, типичное для большинства биологических тканей, с удачным сочетанием и последовательной сменой механизмов деформирования, а именно переходом от деформации путем растяжения относительно «мягких» волокон эластина к деформации более «жестких» коллагеновых белковых структур при больших деформациях. Это отвечает функциональным биомеханическим свойствам тканей и органов, когда при очень малых и малых деформациях важна их податливость и эластичность, а при средних и больших деформациях на первое место выходит прочность. В результате наклон кривой напряжения – деформации не является постоянным. Зависимость от деформации модуля Юнга сводится к тому, что с более высокими значениями деформации ассоциируются более крутые участки кривых σ–ε.

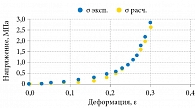
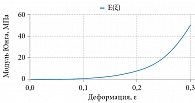
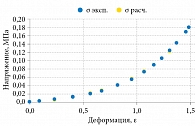
При подборе функциональной зависимости σ = σ(ε) для полученных экспериментальных данных была использована функция genfit, входящая в пакет алгебраических вычислений Mathcad 13. По результатам нелинейной регрессии, функцией, наиболее точно аппроксимирующей полученные данные, оказалась зависимость σ(ε) = 9,918×10^-3exp(18,706ε)-1 МПа (мегапаскалей, 1 Па = 1 Н/м²). Как видно из рис. 1, результаты опыта и расчета мало отличаются друг от друга, средняя погрешность аппроксимации – 0,27. При этом модуль упругости выражался экспонентой E(ε) = dσ(ε)/dε = 0,185exp(18×706ε) МПа и возрастал от E_min = 0,185 при ε = 0 до E_max = 53,278 МПа при ε = 0,3 (рис. 2), среднее значение модуля составило 

 . Отношение E_max/E_min оказалось равным 287,99, что полностью соответствует инкрементальному характеру дифференциального модуля Юнга фиброзной капсулы (увеличиваться при деформировании).

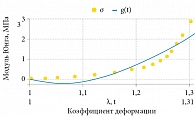
Коэффициенты гиперупругой модели Муни – Ривлина, определенные с помощью функции linfit Mathcad 13, составили C₁₀ = 11,377 и C₀₁ =  12,854 МПа. Проверка согласия между экспериментальными данными и аппроксимирующей кривой (рис. 3) методом Пирсона хи-квадрат не дала оснований для отклонения нулевой гипотезы (на уровне значимости 0,05).

Отметим, что здесь и далее авторы [5] не сообщают методику подготовки образцов аутопсийного материала и образцов in vitro и для испытаний, что затрудняет сравнение результатов их измерений с результатами исследований биомеханических свойств тканей данных органов, полученными другими авторами.

Паренхима почки. Паренхима – основная ткань почки, в норме с низкой эхогенностью. Механические свойства паренхимы почки были исследованы в работе I. Asami и соавт. (1961) [5].

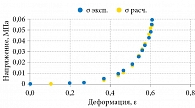
Кривая напряжения – деформации паренхимы почки пациентов в возрасте от 10 до 19 лет показана на рис. 4. Начальная стадия удлинения соответствует около 15% от предела прочности, а начальное удлинение составляет две трети от максимальной деформации.

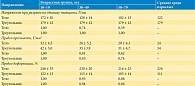
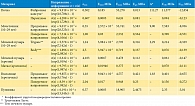
Предел прочности почечной паренхимы максимален у пациентов в возрасте от 10 до 19 лет и уменьшается в возрастной группе от 60 до 79 лет, составляя 69 и 74% от максимальной величины соответственно (табл. 2) [5]. Аналогично изменяется с возрастом и деформация при разрыве.

Значения модулей упругости почечной паренхимы гораздо ниже, чем у соединительнотканной капсулы: E_min= 0,5 кПа, E_ср = 81 кПа, E_max= 626 кПа соответственно. У паренхимы также значительно меньше по величине коэффициенты модели Муни – Ривлина (табл. 9).

Эти результаты согласуются с данными Ю.А. Беловой и Д.Ю. Потапова [6], которые исследовали механические свойства ткани почки с целью моделирования гемостатических швов. Почки с почечными артериями были изъяты у трупов людей обоего пола не позднее 16–18 часов после наступления смерти. Эксперименты проводились в день забора материала, не позднее двух часов после аутопсии. В ходе проведенных экспериментов были определены модули Юнга для тканей почек человека. Полученные данные позволили сделать заключение о механических свойствах различных частей почки. Установлено, что наибольшей упругостью обладает капсула почки, наименьшей – паренхима. Дифференциальный модуль Юнга капсулы равен 40 МПа (при относительной деформации 0,1). Кроме того, был проведен сравнительный анализ деформационно-прочностных свойств почки человека и свиньи. После проведенных исследований в конечно-элементном пакете ANSYS была поставлена двухмерная задача для определения воздействия различных видов швов на ткани почки.

Мочеточник

I. Asami и соавт. (1961) [5] исследовали деформационные свойства мочеточника у 60 пациентов. Мышечная оболочка мочеточника в верхних двух третях состоит из двух слоев гладкомышечных клеток (внутреннего продольного и наружного циркулярного), в нижней трети снаружи появляется третий слой с продольным расположением гладкомышечных клеток.

Предел прочности в обоих (продольном и поперечном) направлениях был наибольшим между 10 и 29 годами и наименьшим между 50 и 79 годами (76%) (табл. 3) [5]. В продольном направлении предел прочности оказался больше в 3,9 раза, чем в поперечном.

Максимальное удлинение в продольном направлении образцов не зависело от возраста. Но в поперечном направлении было наибольшим между 10 и 29 годами, в возрасте от 50 до 79 лет составляло 84% от максимального. Удлинение в поперечном направлении в 2,7 раза превысило таковое в продольном направлении.

Кривые напряжения – деформации в продольном и поперечном направлениях для образцов мочеточника у лиц в возрасте от 10 до 29 лет показаны на рис. 5.

Выраженная анизотропия механических свойств установлена и для модуля упругости: отношение упругих модулей в продольном и поперечном направлениях El_ср/Et_ср = 9,9, что значительно больше единицы (случай упругой изотропии).

Коэффициенты Муни – Ривлина мочеточника составили 7,58 и -8,93 МПа в продольном и 0,39 и -0,55 МПа в поперечном направлении.

Стадия первичного удлинения соответствовала примерно 35% предела прочности в продольном направлении и около 25% – в поперечном. Величина этого удлинения составляет приблизительно пять шестых максимального удлинения в продольном направлении и три пятых – в поперечном.

Мочевой пузырь

Мышечная оболочка мочевого пузыря, непарного полого органа выделительной системы позвоночных животных, расположенного в малом тазу, состоит из трех слоев. При этом в среднем из них большинство гладкомышечных клеток имеет циркулярный ход, в наружном и внутреннем – продольный.

Деформационные свойства тканей мочевого пузыря были исследованы у 59 пациентов (табл. 4) [5]. Авторы изучили основные механические характеристики тела и треугольника Льето мочевого пузыря.

Сравнение возрастных и локальных различий в растягивающей разрывной нагрузке на единицу ширины тела сокращенного мочевого пузыря показало, что наибольшей нагрузка была между 10 и 29 годами, а к 50–79 годам снизилась до 59% от максимального значения. В то же время величина разрывной нагрузки треугольника не показала возрастных изменений. Тело сокращенного мочевого пузыря имеет меньшую разрывную нагрузку, чем у треугольника. При растяжении мочевого пузыря разрывная нагрузка составляет пять седьмых от нагрузки в сокращенном состоянии.

Предел прочности на растяжение сокращенного тела и треугольника мочевого пузыря максимален в возрасте от 10 до 29 лет, но к 50–79 годам прочность снижается примерно до 62 и 74% соответственно по сравнению с таковой в возрасте от 10 до 29 лет. Сокращенное тело мочевого пузыря обладает пределом прочности, равным двум седьмым предела прочности треугольника. Прочность тела одинакова как в сокращенном, так и в растянутом состоянии.

Предельное процентное удлинение сокращенного тела и треугольника мочевого пузыря больше всего в возрастной группе от 10 до 29 лет и меньше всего в возрастной группе от 50 до 79 лет (около 88 и 86% соответственно). Удлинение сокращенного тела в два раза больше, чем у треугольника. В растянутом состоянии мочевой пузырь имеет удлинение, соответствующее пяти шестым от того, который наблюдался в сокращенном состоянии.

На рисунке 6 показаны кривые напряжения и деформации для тела и треугольника мочевого пузыря. Видно, что начальный предел удлинения соответствует около 25% предела прочности. При этом начальное удлинение составляет примерно три четверти от величины конечного удлинения для тела и пять шестых для треугольника. При том же напряжении тело мочевого пузыря имеет гораздо большее удлинение, чем треугольник.

Неоднородность упругих свойств (A) стенок мочевого пузыря может быть выражена безразмерным отношением усредненных модулей Юнга треугольника Et и тела пузыря Eb: Et_ср/Eb_ср = 2,29 (Et_ср = 316 кПа, Eb_ср = 137 кПа), что соответствует более развитому и выраженному мышечному слою треугольника, чем у тела мочевого пузыря. Этот мышечный слой мочевого пузыря, сокращаясь, обусловливает мочеиспускание. Отношение максимальных значений E дает еще большую величину A: Et_max/Eb_max = 3,88 (Et_max = 2,79 МПа, Eb_max = 0,72 МПа).

Коэффициенты модели Муни – Ривлина, рассчитанные с помощью анализа кривых на рис. 6, составили 0,214 и -0,329 МПа у треугольника Льето и 0,076 и -0,139 МПа у тела мочевого пузыря. Эти данные могут быть полезны при проведении математического моделирования искусственных сфинктеров, имплантов и других биопротезов отделов мочевого пузыря при реконструктивных операциях (например, при разработке применяемых в практике урологов сфинктерных протезов из сверхэластичного никелида титана для укрепления сфинктера мочевого пузыря [7]).

Отметим, что, по данным T. Ohara (1953) [8], модуль Юнга мочевого пузыря кролика (Eср = 112 кПа) несколько ниже, чем у человека. При этом предел прочности (42 ± 1,6 Г/мм² у кролика и 24 ± 4,6 Г/мм² у человека) и предел деформации выше (419 ± 17 и 226 ± 26% соответственно). Эти результаты оказались несколько неожиданными, в связи с чем требуется их дополнительное изучение. Возможно, они обусловлены различиями в анатомо-морфологическом строении тканей органов человека и животных или различными экспериментальными условиями.

Уретра

Несмотря на наличие работ, посвященных пассивным биомеханическим свойствам уретры [9], практически отсутствуют количественные данные, характеризующие ее эластичность. Как и ожидалось, для мягких тканей человека и животных наклон кривой напряжения – деформации тканей уретры не является постоянным [10]. Более высокие значения деформации приводят к более крутым кривым, связанным с зависимостью от деформации (модуль Юнга) (рис. 7) [10]. Кроме того, наблюдается хорошо известный гистерезис циклической нагрузки и разгрузки, характеризующий диссипацию энергии внутри ткани при знакопеременных деформациях (наиболее распространенной в механике деформируемого твердого тела является модель линейной упругости; все деформации в рамках данной модели полностью обратимы, диссипации энергии нет, деформации прямо пропорциональны напряжениям). Чтобы оценить модуль Юнга для выбранных значений одноосной деформации, достаточно рассмотреть конечные точки кривой напряжения – деформации. При одноосной деформации 15%-ный модуль Юнга соответствовал только 5 ± 2 кПа. При 35% он возрос до 11 ± 3 кПа. При деформации 45% модуль Юнга достиг 21 ± 4 кПа. В компрессионном эксперименте с применением внутри мочеиспускательного канала давления 41 см H₂O значение модуля Юнга составило 19 ± 5 кПа. Метод аспирации, основанный на растягивающих деформациях, вместе с обратным методом конечных элементов (МКЭ) обеспечил величину модуля 17 ± 5 кПа.

В результате примененные три вида исследования напряженно-деформированного состояния последовательно дали клинически значимые данные о модуле Юнга уретры. Таким образом, оценка соответствует значениям от 10 до 20 кПа. Эти значения сопоставимы с величиной упругого модуля паренхимы почки при малых деформациях, которая была определена в работе J.G. Snedeker и соавт. (2005) [11] как 18 ± 5 кПа.

Часть 2. Репродуктивная система (мужчины)

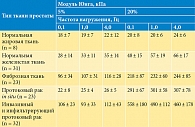
Простата

Авторы исследования [12] (2005) установили, что количественная оценка механических свойств ткани предстательной железы человека важна для разработки соноэластографии при выявлении рака предстательной железы. В исследовании авторы охарактеризовали частотно-зависимый комплексный модуль Юнга нормальных и раковых тканей предстательной железы in vitro с помощью тестирования релаксации напряжения и методов моделирования вязкоупругих свойств тканей. После радикальной простатэктомии из задней области предстательной железы, где часто встречается рак [13], были получены небольшие цилиндрические образцы ткани. Средний возраст пациентов составил 63 года (диапазон 55–76 лет), а средний уровень простатического специфического антигена – 6,1 мкг/мл (диапазон 3,6–9,0). Образцы простаты имели оценку по шкале Глисона 3 + 4 и выше. Образцы перед механическими испытаниями замачивались в физиологическом растворе. Механическое тестирование образцов тканей проводили в течение двух часов после резекции предстательной железы при комнатной температуре. Предполагали, что подготовленные образцы изотропны и однородны. Всего получено и протестировано 17 образцов из восьми человеческих простат. Испытания на релаксацию напряжения на образцах дали повторяемые результаты, соответствующие вязкоупругой дробно-производной модели Кельвина – Фойгта (KVFD) (r² > 0,97). Для нормальных (n = 8) и раковых (n = 9) образцов предстательной железы средние величины комплексных модулей Юнга (|E*|) составили 15,9 ± 5,9 кПа и 40,4 ± 15,7 кПа при 150 Гц соответственно, что дает контраст эластичности 2,6:1,0. Девять двухпробных t-тестов показали наличие достоверных различий между жесткостью нормальной и раковой ткани предстательной железы в одной и той же железе (p < 0,01). По мнению авторов, их исследование вносит существенный вклад в современные знания о вязкоупругих свойствах простаты человека и присущем ей упругом контрасте, создаваемом раком.

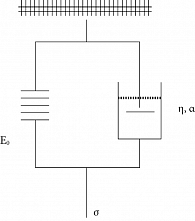
Вязкоупругие свойства мягких тканей обычно моделируются комбинациями идеально упругих и вязких элементов [14]. Помимо трех основных вязкоупругих моделей (модель Максвелла, модель Кельвина – Фойгта и стандартная линейная твердотельная модель), описанных Y.C. Fung (1993) [15], для описания данных механических испытаний также применяли другие линейные, квазилинейные или нелинейные модели. R.C. Koeller (1984) вывел функцию релаксации напряжений с временной зависимостью t–α в функции для модели Кельвина – Фойгта с дробной производной (KVFD) [16]. Со временем большинство исследователей пришли к выводу, что обобщенная модель KVFD (рис. 8) лучше согласуется с экспериментальными данными, чем классическая модель Кельвина – Фойгта.

Устанавливающее уравнение, связывающее напряжение σ(t) с деформацией ε(t) для KVFD-модели, имеет вид:

 (3) 

 где E₀ – модуль упругости (Па);

η = E₀τ^α – коэффициент вязкости (Па×с^α) с постоянной времени τ(с);

α – безразмерное вещественное число между 0 и 1, определяющее порядок производной.

Кривые релаксации (при деформации 5%), обрабатанные в пакете MATLAB Curve Fitting Toolbox, согласуются с расчетными в рамках KVFD-модели. Полученные параметры использованной реологической модели представлены в табл. 5 [12].

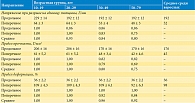
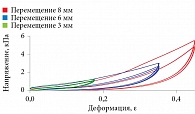
Комплексный модуль Юнга E* в области частот определяли с помощью параметров модели, однако точное значение E₀ = σ(∞)/ε на основании хода кривых релаксации определить не удалось. Но на основании модели были рассчитаны частотно-зависимые модули Юнга нормальных и раковых тканей. Результаты расчета проиллюстрированы на рис. 9. Оказалось, что ткани предстательной железы имеют модули Юнга, которые увеличиваются с частотой в диапазоне соноэластографии.

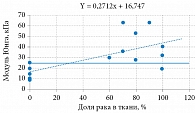
Установлена и исследована более подробно положительная связь между жесткостью тканей (модулем Юнга) и долей рака в тканях (0 и 90%) (рис. 10) [12]. На рисунке показана кластеризация данных о раке предстательной железы, отличающаяся от нормальных значений жесткости. При этом с ростом доли рака в тканях модуль Юнга также увеличивается с градиентом 270 Па на 1% рака. Таким образом, патология мягких тканей сопровождается изменением деформационных свойств, в частности характеристик упругости и вязкости.

Однако S. Phipps и соавт. (2005) [17] сообщили о широком диапазоне (от 40 до 140 кПа) эластического компонента нормальной ткани предстательной железы. По мнению авторов, дивергенция данных вызвана в основном различными вариантами методов испытаний; условиями испытаний, таких как частота компрессии, температура и влажность; вариациями образцов; моделями тканей и другими экспериментальными факторами. В частности, предположение о конкретной реологической модели ткани, например чисто упругой или вязкоупругой, может существенно повлиять на оценку свойств ткани.

Для оценки динамического диапазона эластических свойств тканей, получаемых с помощью эластографии (метод медицинской визуализации, отображающий эластические характеристики и жесткость мягких тканей; твердая или мягкая ткань дает диагностическую информацию о наличии или состоянии заболевания), было исследовано механическое поведение образцов тканей предстательной железы и молочной железы при компрессионной нагрузке [18]. Время между удалением ткани из живого тела и тестированием варьировалось от 25 минут до двух часов, причем ткань охлаждалась от нескольких минут после удаления до начала тестирования. Экспериментальная установка позволяла использовать небольшие образцы, которые можно было считать однородными. Это предположение было подтверждено гистологическим анализом. Образцы были испытаны при трех скоростях деформации, чтобы оценить реологическую природу материала и определить обоснованность моделирования ткани как вязкоупругого материала для интересующих скоростей деформации.

При механической компрессии образца ткани предстательной железы проводилась нагрузка на часть его поверхности. В ходе испытаний регистрировались нагрузка и максимальное смещение, и эти данные использовались в следующем уравнении для определения модуля упругости образцов:

  , (4) 

 где E – модуль упругости;

μ – коэффициент Пуассона;

q – плотность нагрузки (сила на единицу площади);

a – радиус нагруженной области;

w – максимальное смещение в направлении нагрузки.

Предполагается, что образцы тканей несжимаемы с коэффициентом Пуассона μ = 0,495.

При частотах нагрузки выше 1 Гц модуль накопления превысил 93% комплексного модуля.

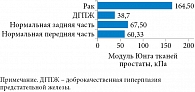
Нормальная ткань предстательной железы имеет более низкий модуль, чем модуль исследуемого рака предстательной железы (табл. 6). Ткань предстательной железы с доброкачественной гиперплазией предстательной железы (ДГПЖ) имела значения модуля упругости значительно ниже, чем нормальная ткань. Наблюдалась постоянная, но не существенная разница в модуле тканей, взятых из передней и задней частей железы.

В результате ткани с ДГПЖ имели значительно более низкие значения (38–41 кПа), чем нормальная ткань; нормальная передняя и задняя части простаты имели значения модуля упругости 55–71 кПа, тогда как рак имел значения 96–241 кПа (табл. 6) [18]. При этом значения модуля Юнга тканей, за исключением раковых (98,33 и 230,67 кПа), не проявили выраженной зависимости от уровня предкомпрессии. Средние значения модуля простаты при различных скоростях деформации (0,1; 1,0 и 4,0 Гц) и степени предварительной компрессии (2 и 4%) представлены на рис. 11.

Таким образом, динамический модуль Юнга может служить диагностическим показателем состояния предстательной железы в норме и при патологии.

Авторы предлагают рассматривать ткани простаты как несжимаемый материал с коэффициентом Пуассона 0,495. Тогда модуль сдвига предстательной железы G_ср = 21,37 Мпа и модуль объемной сжимаемости K_ср = 2130,5 МПа будут соответствовать диапазону гиперупругих материалов (эластомеров).

Кавернозное тело и белочная оболочка

Важной характеристикой эректильной функции полового члена является твердость эрекции (EH – erection hardness). Глобальное обследование в 29 странах показало, что уровень ослабления этой функции составляет около 13–28%. В настоящее время она может оцениваться с помощью валидизированного полуколичественного и простого в использовании показателя эректильной твердости (EHS – erectile hardness score) [19, 20]. Хотя величина EH непрерывно увеличивается во время эрекции и является статистически непрерывной переменной, индекс EHS представляет собой градации по четырехбалльной шкале (рангов). Например, клинически EH полового члена, достигающая третьей степени, означает, что пенис (недостаточно твердый) может быть введен во влагалище во время полового акта. Четвертая степень является максимальной. В работе H. Cheng и соавт. (2020) [21] предложили новый метод количественного измерения EH полового члена в реальном времени с использованием ультразвуковой эластографии сдвиговых волн (SWE – shear wave elastography).

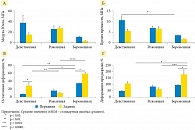
40 пациентам 23–58 лет исследуемой группы с эректильной дисфункцией (ЭД) согласно опроснику IIEF-5 в среднем с 12,5-месячным анамнезом и 20 пациентам в возрасте 25–58 лет контрольной группы в режиме реального времени проводили SWE для измерения жесткости тканей (модуля Юнга) кавернозного тела (corpus cavernosum) и белочной оболочки (tunica albuginea) полового члена во время эрекции, в покое и при различных степенях EH, индуцированных внутрикавернозной инъекцией 5 мкГ простагландина. Исследователи осторожно помещали высокочастотный зонд на вентральный пенис и получали двумерное продольное ультразвуковое (УЗ) изображение пениса, затем переключались в режим SWE, аппарат автоматически устанавливал круговую область 3–5 мм для выполнения процедуры. Частота колебаний УЗ-волн составляла 7,5–15 МГц. Модуль Юнга тканей рассчитывали по формуле E = 3ρc², где ρ – плотность тканей, c – скорость распространения УЗ-волн.

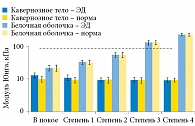
Исследователи не наблюдали существенных различий между пациентами с ЭД и в норме при измерениях SWE, за исключением того, что модуль Юнга кавернозного тела в группе контроля был немного ниже, чем у пациентов с ЭД. Как в исследуемой, так и в конт­рольной группе модуль Юнга незначительно снижался в кавернозном теле в зависимости от степени эрекции (табл. 7, рис. 12):

• в покое: 12,90 ± 2,0/9,82 ± 1,92 кПа;
• степень 1: 10,97 ± 2,26/9,32 ± 1,90 кПа;
• степень 2: 9,25 ± 1,23/9,16 ± 1,71 кПа;
• степень 3: 9,38 ± 1,61/9,18 ± 1,68 кПа;
• степень 4: 9,38 ± 1,47/9,26 ± 1,34 кПа (с градиентом -431,5 Па/-63 Па на одну степень).

Однако жесткость белковой оболочки значительно увеличивалась с ростом EH (в покое: 21,68 ± 4,19/21,59 ± 4,68 кПа; категория 1–4: 32,59 ± 4,19/32,71 ± 3,72; 54,16 ± 8,51/54,12 ± 10,06; 127,82 ± 20,36/127,81 ± 18,10 и 223,93 ± 23,61/223,39 ± 26,82 кПа соответственно). Таким образом, с ростом EHS модуль Юнга кавернозного тела в целом уменьшился на 27,29 и 5,71%, а белочной оболочки – увеличился в 10,33 и 10,35 раза соответственно. Поскольку EH первой и второй степеней клинически означает неспособность совершить половой акт, а EH третьей и четвертой степеней – способность его реализации, точка отсечения для модуля Юнга белочной оболочки для оценки возможности исполнения полового акта составляет 81,60 кПа (рис. 12).

По мнению авторов, жесткость белочной оболочки, а не жесткость кавернозного тела обеспечивает хороший показатель индекса клинической визуализации для оценки EH полового члена. Жесткость белочной оболочки постоянно менялась во время эрекции полового члена, что можно было количественно измерить с помощью SWE. По сравнению с EHS измерение модуля Юнга белочной оболочки полового члена с помощью SWE является новым и объективным методом количественной оценки EH (p < 0,05). Благодаря объективным и поддающимся количественной оценке характеристикам измерение модуля Юнга позволяет более точно, чем EHS, выполнить диагностику и оценить влияние на EH различных методов лечения ЭД.

По данным [22], для tunica albuginea при средней толщине 2,4 мм и растягивающем напряжении 200 кПа модуль Юнга равен 12 МПа, а коэффициент Пуассона – 0,4.

Тестикула

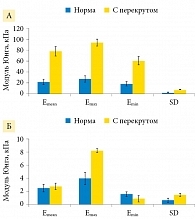
SWE – это недавно разработанный метод, позволяющий получить жесткость тканей и органов с помощью отслеживания распространения сдвиговых волн через структуру. Несколько исследований продемонстрировали его потенциал в дифференциации между больной и нормальной тканью в клинической практике, однако применимость к заболеваниям яичек не была выяснена. S. Zhenxing и соавт. (2015) [23] исследовали целесо­образность и воспроизводимость SWE при перекруте яичек. Под перекрутом яичка понимают перекручивание семенного канатика, приводящее к его ущемлению и нарушению кровоснабжения яичка. В этом проспективном исследовании приняли участие 15 пациентов с полным перекрутом яичек, перенесших орхиэктомию. Сравнивали результаты, полученные при SWE, наряду с общепринятой серошкальной и цветной допплеровской сонографией. Результаты показали, что (i) размер поврежденного яичка был увеличен, а скрученная паренхима яичка была гетерогенной. Сигналы кровотока в поврежденном яичке были едва заметны или отсутствовали; (ii) модуль Юнга, включающий значения E_mean, E_max, E_min и SD в пограничной зоне перекрученного яичка, был выше, чем у нормального яичка (E_mean = 78,07 ± 9,01 кПа против 22,0 ± 5,10 кПа; E_max = 94,07 ± 6,53 кПа против 27,87 ± 5,78 кПа; E_min = 60,73 ± 7,84 кПа против 18,90 ± 4,39 кПа; SD = 7,67 ± 0,60 кПа против 2,30 ± 0,36 кПа; p < 0,05); значения E_max и SD в центральной области перекрученного яичка были выше таковых в соответствующей области нормального яичка (E_max = 8,23 ± 0,30 кПа против 3,97 ± 0,95 кПа; SD = 1,5 ± 0,26 кПа против 0,67 ± 0,35 кПа; p < 0,05), а значения Emin были ниже, чем у нормальных яичек 0,93 ± 0,51 кПа против 1,6 ± 0,36 кПа; p < 0,05) (рис. 13). Однако средние значения E_mean в центральной области яичка с перекрутом и нормального яичка статистически не отличались (2,77 ± 0,50 кПа против 2,53 ± 0,59 кПа; p > 0,05).

Авторы работы сделали вывод, что SWE является неинвазивным, удобным и хорошо воспроизводимым методом и может служить важным альтернативным инструментом в диагностике и мониторинге прогрессирования патологии мошонки в дополнение к традиционной допплерографии.

Целью исследования [24] было оценить значение и эффективность применения в клинической практике SWE в реальном времени нормальной паренхимы яичек и различных распространенных заболеваний яичек.

Материал и методы включали проведение SWE 338 пациентам (средний возраст – 43,2 ± 17,2 года, диапазон – 17–78 лет) в составе нормальных семенников (n = 358), c тестикулярным микролитиазом (n = 40), а также с различными заболеваниями яичка (n = 208) и определение жесткости тканей. Статистическую оценку проводили для определения порога жесткости при патологической диагностике.

Средний размер очагов поражения яичек составил 2,6 ± 1,5 см (диапазон – 10–42 мм). Среднее значение модуля Юнга для нормального яичка было зафиксировано на уровне 4,55 ± 2,54 кПа. Независимо от стадии микролитиаза регистрировали более высокое статистически значимое значение упругого модуля. При остром орхите среднее значение жесткости было несколько выше, но статистически незначимо. Опухолевые процессы яичек имели среднее значение модуля 21,02 кПа с отсечением 16,1 кПа. Фиброз показал самое высокое медианное значение жесткости – 30,03 кПа при отсечении 26,3 кПа. При анализе распределения различных патологических групп была выявлена статистически значимая разница между фиброзом и опухолевыми процессами (p = 0,001).

Авторы сделали вывод, что SWE является целесообразным методом исследования паренхимы яичек. Значения SWE могут быть использованы для достоверной дифференциации фиброза яичек и опухолевого процесса.

Часть 3. Репродуктивная система (женщины)

Матка

Деформационные свойства матки нескольких крольчих были изучены T. Ohara (1953) [8].

Матка кроликов имела разрывное напряжение на единицу толщины в продольном направлении 24 Г/мм, предел прочности 18 ± 0,7 Г/мм² и деформацию при разрыве (предельную деформацию) 150 ± 6,8%. Кривая напряжения – деформации представлена на рис. 14.

В работе R. Oda (1952) [25] определены деформационные свойства матки восьми крольчих.

Образцы матки выявили предел прочности при расширении 1,3 ± 0,33 кГ/см², предельную силу расширения на единицу толщины 1,4 кГ/см²/мм и предельное расширение при диаметре матки 7 мм 0,096 ± 0,0015 мл.

Упругие модули Юнга стенки матки крольчих составили E_min = 0,0194 МПа, E_max = 0,375 МПа, E_ср = 0,119 МПа, а коэффициенты Муни – Ривлина C₁₀ и C₀₁ – 0,078 и -0,111 МПа соответственно. Аппроксимирующая опытную кривую напряжения – деформации функция имеет вид σ(ε) = 9,795×10^-3.(exp(1,987.ε) - 1) и имеет самую низкую среди исследованных урогенитальных тканей среднюю погрешность аппроксимации 0,04.

Механическая функция матки имеет решающее значение для защиты плода во время здоровой беременности. Ранняя сократительная активация ткани матки может привести к преждевременным родам (ПР). В 2014 г. 9,56% беременностей заканчивались ПР. Это также является основной причиной смерти детей в возрасте до пяти лет. Характеристика материальных свойств ткани матки важна для понимания механических повреждений матки и причин возникновения ПР.

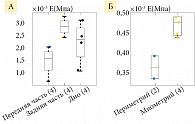
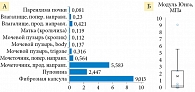
В исследовании [26] у 28 пациенток, перенесших гистероэктомию, взяли 78 образцов матки и провели тест на наноиндентирование. Возраст пациенток на момент сбора данных колебался от 39 до 49 лет, диапазон паритета – от 0 до 12. Сразу же после экстирпации взяли образцы каждой из трех локализаций матки: передней, задней и дна. Все образцы охватывали ширину стенки матки (от 15 до 25 мм) и занимали площадь квадратного поперечного сечения с длиной края от 10 до 15 мм. Все образцы были мгновенно заморожены с использованием сухого льда и хранились в морозильной камере при температуре -80 °C до механических испытаний. Перед каждым испытанием образцы размораживали при комнатной температуре в течение двух часов в фосфатно-буферном физиологическом растворе. Затем каждый образец был разделен на 4–8 срезов параллельно стенке матки. Обратный МКЭ проводился для подгонки четырех параметров материала к экспериментальным данным, среди которых основные: модуль Юнга E, коэффициент Пуассона ν и коэффициент жесткости волокон. Внутри каждой матки наблюдали значительные различия в модуле Юнга и коэффициенте Пуассона в разных местах и слоях, что указывало на неоднородность свойств материала матки человека.

Модуль Юнга E передней стенки матки был значительно меньше, чем задней (рис. 15 А). Отношение Пуассона в периметрии был значительно меньше, чем в миометрии (рис. 15 Б) [26].

Несмотря на всплеск интереса к исследованиям в области репродуктивного здоровья женщин, большинство исследований по-прежнему ограничивалось акушерством и гинекологией без приобщения знаний из сообщества биомехаников. Таким образом, механика женской репродуктивной системы и изменения, обусловленные беременностью, возрастом, ожирением и различными заболеваниями, до конца не изучены.

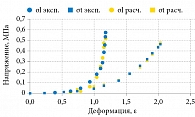
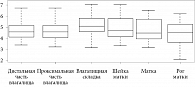
А. Baah-Dwomoh и соавт. (2016) [27] рассмотрели методы испытаний для характеристики механических свойств репродуктивных органов и поддерживающих структур женского тазового дна. Они включали стандартные методы испытаний, такие как одноосные испытания, испытания на сжатие и двухосные испытания, а также аспирационные и ультразвуковые испытания. На рисунке 16 представлен ряд данных по упругим модулям, организованный по органам/тканям [28–44].

Представленные на рисунке модули упругости были получены путем рассмотрения разных типов образцов. Поскольку исследовали нормальные и пролапсированные ткани беременных и небеременных, людей и животных, старых и молодых, а также применяли методы in vivo и ex vivo, наблюдалась большая вариабельность данных. Модуль упругости действительно мог быть выбран для сравнения, так как является наи­более известным механическим параметром во всех типах испытаний, для всех органов и структур. Модули упругости находились в диапазоне 0,02–1,4 МПа для матки, 2,5–30 МПа – для влагалища, 2,17–243 кПа – для шейки матки, 0,75–29,8 МПа – для маточно-крестцовой связки, 0,5–5,4 МПа – для кардинальной (главной) связки и 9,1–14,0 МПа – для круглой связки. Так называемая круглая связка поддерживает антефлексио матки. Это положение матки, когда она начинается от своего относительно широкого основания латерально к внутреннему паховому кольцу и заканчивается в больших половых губах. Отметим, что в изучаемых нами работах не изучались упругие свойства половых губ (labia minora или labia majora), равно как и девственной плевы (hymen).

Следует также отметить, что анатомическое расположение исследуемых образцов в репродуктивных органах и поддерживающих тканях контролировалось или сообщалось не во всех работах. В нескольких исследованиях показано, что механическая реакция образцов тканей может значительно меняться в зависимости от их анатомического расположения в репродуктивных органах. Например, показатели жесткости шейки матки варьируются по ее длине. Аналогично модули, предел прочности при растяжении и деформация на пределе прочности при растяжении, а также вязкоупругие свойства были различными для разных областей комплекса маточно-крестцовой (МКС)/кардинальной связки (КС). Для лучшего понимания потенциальной изменчивости в зависимости от локализации ткани или органа были проведены более точные сравнения между опубликованными исследованиями.

Влагалище

T. Ohara (1953) [8] исследовал растягивающие свойства стенки влагалища нескольких крольчих. Ткани имеют разрывную нагрузку на единицу ширины образцов в продольном направлении 73 Г/мм, предел прочности на разрыв – 57 ± 4,2 Г/мм² и предел относительного удлинения – 113 ± 15%. В поперечном (радиальном) направлении нагрузка на разрыв при растяжении составила 59 Г/мм, предел прочности на разрыв – 46 ± 3,7 Г/мм² и предел относительного удлинения –  194 ± 14%. На рисунке 17 показаны кривые напряжения – деформации стенки влагалища крольчих в продольном и поперечном направлениях. Предел начального удлинения соответствует примерно 20% от предела прочности для обоих направлений.

Начальное удлинение составляет примерно пять шестых от конечного удлинения в продольном направлении и две трети в поперечном направлении. Дифференциальный модуль Юнга стенок влагалища был инкрементальным, то есть увеличивался по мере растяжения тканей от минимального значения E_min = 9,043 × 10^-5 МПа при ε = 0 до максимального E_max = 4,557 МПа при ε = 1,18 в продольном направлении (среднее значение E_ср = 0,421 МПа) и от минимального значения E_min = 0,017 МПа при ε = 0 до максимального E_max = 0,948 МПа при ε = 2,04 в поперечном (среднее значение модуля E_ср = 0,23 МПа). Коэффициент упругой анизотропии, определенный как безразмерное отношение модулей упругости в продольном и поперечном (радиальном) направлениях стенки влагалища, составил: El_ср / Et_ср = 1,83. Коэффициенты Муни – Ривлина составили 0,401 и -0,655, а также 0,156 и -0,272 МПа соответственно.

Вагинальная тактильная визуализация (ВТВ) основана на принципах, аналогичных принципам ручной пальпации. Целью исследования [45] стало определение клинической пригодности нового подхода к визуализации и количественной оценке эластичности тканей в нормальных условиях и с пролапсом.

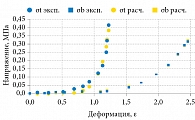
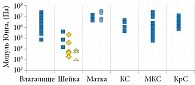
В исследовании приняла участие 31 женщина. Средний возраст составил 60 ± 17 лет (от 28 до 90). Эластичность ткани (модуль Юнга) стенок влагалища рассчитывали по пространственному градиенту напряжений в полученных трехмерных тактильных изображениях.

Авторы наблюдали выраженную вариабельность эластичности тканей. Диапазон упругости в апикальной части передней стенки влагалища варьировался от Е = 2,5 до 15,8 кПа (дисперсия ±4,3 кПа), а для задней стенки – от Е = 2,5 до 13,5 кПа (дисперсия ±3,1 кПа) в норме. Эта изменчивость существенно превышает точность измерений. По результатам исследований, средние значения эластичности тканей передней (рис. 18) и задней стенок влагалища в нормальных условиях составили 7,4 ± 4,3 и 6,2 ± 3,1 кПа соответственно. При пролапсе третьей стадии средние значения эластичности тканей переднего и заднего компартаментов влагалища резко снижались и составляли 1,8 ± 0,7 и 1,8 ± 0,5 кПа соответственно.

Установлены также отличия в эластичности передней и задней стенок влагалища женщин. Эта разница статистически значима, что подтверждено как визуальным сравнением доверительных интервалов для представленных выборочных медианных значений, так и тестированием Analysis of Variation (ANOVA) (p < 0,0001).

Авторы заключили, что ВТВ может применяться для трехмерной визуализации влагалища и количественной оценки эластичности вагинальной ткани, поскольку предоставляет важную информацию для дальнейшего понимания пролапса тазовых органов и хирургического лечения.

Целью работы [46] было проведение комплексного анализа биохимического состава тканей и пассивных биомеханических свойств влагалища овец и его соотношения с гистоархитектурой на различных репродуктивных стадиях в рамках создания большой доклинической модели животных для оценки подходов регенеративной медицины к хирургическому лечению пролапса тазовых органов.

Вагинальную ткань изучали у девственниц (n = 3), рожавших (n = 6) и беременных овец (n = 6; средняя гестация – 132 дня). Все животные были гуманно усыплены в соответствии с действующими рекомендациями путем внутривенного введения пентобарбитала натрия в яремную вену (150 мг/кг). Анализировали гистологию тканей, биохимию белков внеклеточного матрикса для количественного определения общего коллагена и измерения соотношения коллагена III/I + III, выполняли аминокислотный анализ для количественного определения эластина. Модуль Юнга, напряжение и деформацию, остаточную деформацию после циклического нагружения определяли с помощью одноосной тензометрии.

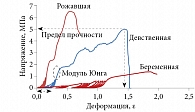
Вагинальная ткань девственных овец имела самое низкое общее содержание коллагена и величину остаточной деформации. У рожавших ткани демонстрировали наибольшее содержание общего коллагена и наименьшее – эластина с сопутствующим высоким пределом прочности. Напротив, беременные овцы имели самое высокое содержание эластина и самое низкое содержание коллагена, а также самый толстый гладкомышечный слой, что обусловило низкий предел прочности и плохое восстановление размеров после повторяющихся нагрузок (рис. 19 и 20) [46].

Авторы установили, что влагалище беременной овцы было наиболее растяжимой, но самой слабой тканью, тогда как ткани рожавших и девственных животных были крепкие и эластичные. Биохимические изменения в белковом составе тканей коррелировали с вариациями биомеханических свойств. Беременность оказала наибольшее влияние на состав тканей и биомеханические свойства, как это было продемонстрировано и для других видов.

Киты, дельфины и морские свиньи имеют необычные вагинальные складки неизвестной функции, которые, как предполагается, играют важную роль в половом созревании. Потенциальную функцию вагинальных складок оценивали с помощью тестирования механических свойств тканей репродуктивного тракта обыкновенных афалин (Tursiops truncatus) в шести различных регионах и разных возрастных классах у посмертных образцов. В исследовании [47] оценивали эффективный модуль упругости тканей с помощью испытаний на вдавливание путем наноиндентирования и растяжения образцов. Исследовали нелинейные механические реакции биологических тканей, которые нечасто поддаются количественной оценке.

Размороженные образцы перед испытаниями содержали в 1%-ном буферном физиологическом растворе. Процесс замораживания/размораживания может поставить под угрозу микроструктуру ткани, поэтому предпринимали все усилия по уменьшению ее деградации. Все измерения проводили ex vivo в помещении с температурой, поддерживаемой приблизительно на уровне 20 °C. Соответственно ожидалось, что потеря воды и изменения в тканях во время эксперимента будут идентичны во всех образцах.

Самая жесткая ткань была в области влагалищной складки (рис. 21) [47] и в целом жестче у половозрелых животных по сравнению со зрелыми, что, вероятно, отражало биомеханические адаптации, связанные с совокуплением и родами. Данные подтверждают гипотезу, что вагинальные складки могут обеспечить женщинам механизмы снижения копулятивного воздействия на другие репродуктивные ткани. Исследование, по мнению авторов, дает представление о том, как ткани женских половых органов могут функционировать во время совокупления.

Яичники

По мнению A. Ansardamavandi и соавт. (2020) [48], исследовавших ткани яичников с патологическими состояниями гистологически и с помощью методов атомно-силовой микроскопии (АСМ), различные заболевания влияют как на морфологические, так и на механические характеристики пораженной ткани, способствуя усилению симптомов.

В наномеханическом исследовании с помощью АСМ охарактеризована эластичность тканей яичников человека с четырьмя различными патологическими состояниями: муцинозными, серозными и зрелыми тератомными опухолями и неопухолевым эндометриозом.

Образцы ткани яичников были получены во время операций у женщин с различными заболеваниями яичников после получения письменного информированного согласия пациенток под наблюдением эксперта-онколога в соответствии с процедурой проведения экспериментов с участием людей. Экспертом-патологом исследованы биоптаты и отобраны гладкие однородные участки органов с лучшими характеристиками и без физических повреждений. Для проведения АСМ-тестов тщательно вырезали образцы размером 0,3 × 1 × 1,5 см, остальные использовали для патологоанатомических исследований. Изученные патологом тестовые образцы определены как пораженные эндометриозом, муцинозная цистаденома, серозная цистаденома и зрелая тератома.

Кривые наномеханических испытаний σ–ε были количественно обработаны и полученные данные классифицированы методом кластеризации K-средних, а также нечетких C-средних для оценки модулей упругости клеточных и внеклеточных частей больных тканей и их сравнения при четырех болезненных состояниях. Образцы окрашивали гематоксилин-эозином для дальнейшего гистологического изучения различных локализаций тканей.

Авторами установлено, что патологическое состояние значительно влияло на механические свойства тканей яичников. Наблюдались значительные изменения упругих модулей как клеточных, так и внеклеточных частей. Зрелые тератомные опухоли, обычно состоящие из нескольких типов клеток и гетерогенной структуры внеклеточного матрикса, имели самый широкий диапазон показателей эластичности и самую большую жесткость тканей со средним модулем упругости 14 кПа (рис. 22) [48]. Образцы серозных опухолей представляли собой самые мягкие ткани с модулем упругости всего 400 Па для клеточной части и 5 кПа для внеклеточного матрикса. Ткани при двух других заболеваниях были близки по механическим свойствам. Так, муцинозные опухоли были незначительно жестче эндометриоза в клеточной части (1300 Па по сравнению с 1000 Па), со средним модулем упругости внеклеточного матрикса 8 кПа для обоих типов тканей.

A. Ansardamavandi и соавт. (2020) [48] сделали вывод, что высокая частота развития карцином из тератом и серозных опухолей может быть связана с интенсивным изменением механических особенностей клеточного и внеклеточного матрикса, служащих в качестве потенциального фактора риска, и требует дальнейшего изучения.

Статистическое применение ANOVA показало, что количественная разница между показателями эластичности при заболеваниях статистически значима (p < 0,05), за исключением разницы между жесткостью тканей при эндометриозе и тканей с муцинозными опухолями.

Молочная железа

Результаты изучения механических параметров образцов тканей молочной железы [18] представлены в табл. 8 [18].

В таблице 8 показано, что жировая ткань молочной железы имеет постоянный модуль в тестируемом диапазоне деформаций, в то время как другие ткани имеют модуль, зависящий от уровня деформации. Образцы фиброзной ткани из молочной железы оказались на один-два порядка жестче жировой ткани. Обнаружено, что нормальная железистая ткань молочной железы имеет эластический модуль, подобный модулю жира при низких уровнях деформации, но модуль железистой ткани на порядок выше жировой при высоких уровнях деформации. Карциномы молочной железы жестче, чем другие ткани, на более высоком уровне деформации; внутрипротоковые карциномы in situ похожи на жировую ткань на низком уровне деформации и намного жестче, чем жировая и железистая ткани, при высоких деформациях. Инфильтрирующие протоковые карциномы намного жестче, чем любые другие ткани молочной железы (рис. 23).

Пуповина

K. Katake (1961) [49] первым исследовал биомеханические свойства оболочки пуповины – эластичного и достаточно прочного «канатика», соединяющего плод с организмом матери. Было изучено 62 плода.

Средняя разрывная нагрузка при растяжении неповрежденной пуповины оказалась наибольшей на 10-м месяце беременности и оценена в 10 ± 0,3 кГ у зрелых плодов. Разрывная нагрузка на растяжение в течение четвертого месяца составляет одну шестнадцатую, пятого – одну пятую, шестого – две пятых, седьмого – половину, восьмого – пять седьмых и в течение девятого месяца – пять шестых разрывной нагрузки, соответствующей 10-му месяцу.

Средняя разрывная нагрузка неповрежденной пуповины в 15 раз превышает массу тела плода на четвертом месяце беременности, в 12 раз – на пятом, в восемь раз – на шестом, в шесть раз – на восьмом, в четыре раза – на 10-м месяце и в три раза – у зрелых плодов.

Предел прочности пуповины на растяжение наибольший на 10-м месяце и оценивается в 150 ± 5 Г/мм² у зрелых плодов. На четвертом месяце она составляет одну пятую, пятом – одну четвертую, шестом – половину, седьмом – три пятых, восьмом – пять седьмых, а на девятом месяце – девять десятых от прочности на 10-м месяце беременности.

На 10-й месяц беременности также приходится наибольшее предельное удлинение (оценивается в 59 ± 2%) (рис. 24). Две трети от этой величины отмечено у плодов после четвертого месяца, три четверти – шестого, девять десятых – восьмого месяца беременности. Половые отличия в деформационных свойствах пуповины плодов не выявлены.

Установлено, что предел начального удлинения пуповины соответствует приблизительно 30% от предела прочности, а начальное удлинение составляет пять шестых от предела удлинения. Удлинение при том же напряжении увеличивается с возрастом плода.

Разрыв сначала образуется в виде щели глубиной несколько миллиметров и длиной около 10 мм по оси пуповины с последующими косыми трещинами на концах разрыва. Разрывы чаще возникают в эмбриональной трети пуповины, хотя иногда они появлялись в средней и плацентарной третях.

Значения модулей упругости пуповины достаточно высоки и ненамного ниже, чем у соединительнотканной капсулы почки: E_min = 0,0083 МПа, E_ср = 2,4475 МПа, E_max = 18,905 МПа соответственно. У пуповины также весьма значительны и коэффициенты Муни – Ривлина – C₁₀ = 2,35 и C₀₁ =  3,01 МПа (табл. 9).

Данные расчетов деформационных свойств тканей, полученные путем анализа кривых механических испытаний σ = σ(ε) [5, 8, 25, 49], представлены в табл. 9 и на рис. 25.

Выводы

1. Упругость и прочность урогенитальных тканей определяются свойствами эластиновых и коллагеновых комплексов с существенно нелинейной зависимостью деформации от напряжения. Зависимости механического напряжения – деформации тканей могут быть описаны экспоненциальной функцией  σ = α(e^βε-1), а модуль Юнга – E = αβe^βε, где α и β – численные параметры, определяемые для каждого типа ткани отдельно. В результате пассивные биомеханические свойства урогенитальных тканей являются упруговязкими (вязкоупругими), а модуль Юнга – дифференциальным и инкрементальным (увеличивающимся при деформировании).

2. Диапазон значений упругих свойств (модуль Юнга) урогенитальных тканей весьма широк – от 18 ± 7 кПа (жировая ткань молочной железы) и 36 ± 9 кПа (ДГПЖ) до 5,58 ± 0,10 МПа (мочеточник в продольном направлении) и 9,01 ± 0,13 МПа (фиброзная капсула почки) (M ± SD), что, очевидно, связано со значительной разницей в морфологии тканей и их функциональной нагрузкой. При этом константы гиперупругих моделей Муни – Ривлина C₁₀ и C₀₁ изменяются от 0,094 и -0,123 МПа (паренхима почки) до 11,377 и -12,854 МПа (фиброзная капсула).

3. Разброс значений параметров механических свойств тканей и органов вызван их нелинейностью, неоднородностью и анизотропией, а вариабельность, по данным различных авторов, может быть обусловлена неодинаковыми экспериментальными условиями.

4. Оценка эластичности может служить диагностическим показателем состояния урогенитальных тканей в норме и при патологии, например, жесткость тканей предстательной железы зависит от ее статуса – наличия гиперплазии и процента рака в исследованных образцах (p < 0,01), эластичность вагинальной ткани – наличия и стадии пролапса тазовых органов (p < 0,0001), а жесткость белочной оболочки – эректильной твердости по шкале EHS (p < 0,05).

5. Коэффициенты гиперупругих моделей Муни – Ривлина C₁₀ и C₀₁ могут быть полезны при математическом моделировании напряженно-деформированного состояния тканей органов урогенитальной зоны, а характеристики деформационных свойств тканей – при реконструктивных вмешательствах и разработке эндопротезов (стентирования уретры, лечения сфинктерного аппарата мочевыводящей системы, пролапса тазовых органов, эректильной дисфункции и др.).