Исследование качества жизни больных раком предстательной железы с помощью опросника EORTC QLQ-PR25 на основе классической и современной теорий тестирования

Таблица 1. Структура опросника EORTC QLQ-PR25

Рис. 1. Стартовое окно диалоговой системы ИЛП

Таблица 2. Возраст и характеристики ПСА больных

Рис. 2. Возраст больных, лет (А); сумма баллов по Глисону (Б, В)

Рис. 3. ПСА больных меньше 35 нг/мл (А); соотношение f/t свободного и общего ПСА (Б)

Рис. 4. Средний исходный («сырой») балл больных при опросе (А); сумма приведенных баллов согласно классической теории тестирования (Б)

Таблица 3. Структура вариантов ответов респондентов

Рис. 5. Структура балльных показателей ответов респондентов по шкалам

Рис. 6. Частота симтомов и КЖ, 0–100%

Таблица 4. Интерпретация показателя альфа Кронбаха

Таблица 5. Альфа Кронбаха, корреляционные связи и success scaling шкал опросника

Рис. 7. Логистическая функция Pij

Таблица 6. Значения Pij в зависимости от соотношения θi и βj

Рис. 8. Схема противодействия латентных переменных в медицине

Таблица 7. Характеристика индикаторов

Рис. 9. Характеристические кривые индикаторов. Число подгрупп объектов: десять (фрагмент)

Рис. 10. Характеристические кривые индикаторов 1 (А) и 11 (Б). Число подгрупп объектов: три

Таблица 8. Результаты расчета порогов кривых распределения категорий

Рис. 11. Кривые распределения категорий (фрагмент)

Таблица 9. Характеристика объектов

Рис. 12. Местоположение латентных переменных

Рис. 13. Диапазон изменения латентных переменных в представлении “Box and whiskers”

Рис. 14. Качество жизни, измеренное методами КТТ и с помощью диалоговой системы ИЛП (современной теории тестирования)

Рис. 15. Качество жизни, измеренное методами КТТ и с помощью диалоговой системы ИЛП (современной теории тестирования)

Таблица 10. Матрица оценок ответов пациентов (фрагмент)

Рис. 16. Виджет программы ИЛП, цветами обозначены категории, которые были выбраны объектами в исходной матрице ответов (см. табл. 9)

Таблица 11. Матрица вероятностей ответов пациентов (фрагмент)

Рис. 17. Виджет программы ИЛП, иллюстрирующий степень соответствия наблюдаемых значений теоретическим (см. табл. 10)

Рис. 18. Кривые распределения категорий для политомической переменной (0, 1, 2, 3)

Введение

Понятие качества жизни (КЖ), появившееся в научной литературе в XX веке, представляет собой сводную характеристику физического, психологического, эмоционального и социального функционирования больного человека, основанную на его субъективном восприятии [1]. Несмотря на то что стандартных норм и критериев исследования КЖ не существует, общепринятыми и основными инструментами для изучения КЖ служат опросники, составленные с помощью психометрических методов.

Понятие «качество жизни» в полной мере применимо и к онкоурологии. Рак предстательной железы (РПЖ) – один из наиболее распространенных видов рака у мужчин. Его исследованию и методам лечения посвящено большое число работ [2, 3]. Рак простаты имеет относительно хороший прогноз среди других видов рака. Продолжительность жизни 90% пациентов, у которых он был диагностирован на первой или второй стадии, составляет 15 лет и более, а пятилетняя выживаемость может достигать 70% [4]. Длительная выживаемость означает, что КЖ является важным показателем успеха лечения выживших. С учетом того что рак простаты в большинстве случаев прогрессирует медленно, сегодня все большее значение в выборе тактики лечения рака простаты имеет мнение пациента [5]. По мнению авторов [6], вопросы определения КЖ у онкологических больных с РПЖ имеют немаловажное значение при выборе метода лечения. При этом поиск новых подходов к исследованию КЖ больных со злокачес­твенными опухолями мочевыделительной системы играет важную роль как в клинических исследованиях, так и в повседневной практике онкоурологических отделений.

Тестология как наука о создании научно обоснованных измерительных методик рассматривает две теории: классическую и современную. В отечественной медицинской литературе для анализа КЖ применяется в основном классическая теория тестирования (КТТ), в зарубежной же преобладает современная теория тестирования Item Response Theory (IRT), представляющая собой часть более общей теории латентных переменных. Многие переменные являются латентными, то есть скрытыми, непосредственно не измеряемыми. Такие переменные задаются через набор индикаторов, представляющих собой пункты опросника или задания теста, которые можно непосредственно оценить [7]. Используемые в теории латентных переменных модели носят вероятностный характер и предполагают, что существует одномерный континуум, на котором имеет место стохастическое распределение латентных переменных с определенной плотностью. Мировой опыт измерения латентных переменных рекомендует использование модели Раша (Rasch model) [8], в которой «вероятность успеха» описывается логистической функцией и которая сейчас проходит период становления в России. В настоящей работе параметры КЖ пациентов интерпретированы и с помощью классической теории, и с помощью теории латентных переменных.

Материал и методы

В онкологической практике часто применяется общий опросник КЖ Европейской организации по исследованию и лечению рака (European Organization for Research and Treatment of Cancer Quality of Life Questionnaire) EORTC QLQ-C30. Он содержит 30 вопросов и является наиболее популярным инструментом, используемым в рандомизированных контролируемых исследованиях КЖ пациентов с раком. При этом для оценки проблем КЖ пациентов с раком простаты EORTC разработан дополнительный модуль EORTC QLQ-PR25. Специальный модуль QLQ-PR25 оценивает симптомы мочеиспускания, кишечные симптомы, симптомы, связанные с гормональным лечением, сексуальную активность и сексуальное функционирование. Результаты международной проверки модуля были опубликованы в 2008 г. в работе [9], а пилотные валидационные исследования EORTC QLQ-C30 и QLQ-PR25 в Испании, опубликованные в 2008 г. в работе [10] и в 2009 г. в работе [11], показали, что эти инструменты имеют удовлетворительные психометрические свойства, надежность и валидность. В исследовании [11] опрашивали больных со статусом по шкале Карновского (Karnofsky scale) 91,8–96,1. В исследовании [12] было установлено, что тайваньско-китайская версия EORTC QLQ-PR25 вполне уместна для оценки состояния пациентов с раком простаты. Однако структура шкал этого модуля и дифференциальная способность шкалы кишечных симптомов оставляли желать лучшего. Валидность шкал для различных клинических состояний была приемлемой, но менее удовлетворительной, чем у EORTC QLQ-C30. По мнению авторов, некоторые вопросы модуля, возможно, требуют изменения, чтобы точнее отразить проблемы пациентов.

Согласно руководству [13], модуль EORTC QLQ-PR25 состоит из 25 вопросов (табл. 1), охватывающих шесть шкал: PR URI (симптомы мочевой системы, восемь пунктов); PR AID (помощь при недержании мочи, один пункт); PR BOW (кишечные симптомы, четыре пункта); PR HTR (симптомы, связанные с гормональной системой, четыре пункта). Семь пунктов – это условные вопросы, обусловленные потребностью в помощи при недержании мочи (Q38, PR8) и статусом сексуальной функции (Q50–55, PR20–25). Мы посчитали логичным и допустимым сгруппировать шкалы PR URI и PR AID, а также PR SAC и PR SFU в две обобщенные шкалы и в итоге рассматривать четыре укрупненные симптоматические шкалы: 1 – симптомы мочевыделительной системы; 2 – симптомы патологии кишечника; 3 – гормональные симптомы, связанные с заболеванием; 4 – способность к репродукции (сексуальная активность и сексуальная функция).

Анкета заполнялась последовательно с первого по 25-й вопрос (пункт), на каждый вопрос (пункт) опросника мог быть дан только один ответ. Возможные градации ответов на вопросы анкеты – от 1 до 4 («Совсем нет», «Немного», «Довольно часто», «Очень часто»). Таким образом, градации ответов представляли собой частоты встречаемости определенного специфического симптома, фигурирующего в пункте опросника. За исключением трех вопросов (PR20–22) больший балл соответствовал худшему состоянию здоровья. При подсчете общей суммы баллов полученные при опросе первичные («сырые») баллы RS (Raw Scores) за ответы по пунктам PR20–22 перекодировали в приведенные по алгоритму 5-RS, то есть модифицировали ключи к тесту – связь ответов с присваиваемыми баллами. По каждому пункту вычисляли среднее по всем пациентам значение исходного («сырого») балла. Далее для каждой из укрупненных шкал (i = 1, 2, 3, 4) баллы снова усредняли уже по пунктам до RS_i и линейно нормировали по формуле S_i = 100 × (RS_i - Мин) / R, где R = Макс - Мин = 4 - 1 = 3 – диапазон (Range) изменения баллов, что в итоге позволило вычислить интегральный индекс качества жизни (ИКЖ):

QoL (ИКЖ) = 100 - Среднее (S_i), %, (1)

В результате для функциональных симптоматических шкал наилучшее состояние здоровья пациента соответствовало 0, наихудшее – 100%. Для шкалы общего статуса здоровья, наоборот, наилучшее состояние пациента соответствовало 100%, наихудшее – 0%.

При обработке матрицы данных (100 × 25) применяли диалоговую систему ИЛП, альтернативную зарубежным аналогам RUMM (Австралия) и Winsteps (США) (рис. 1). Как известно, данная система позволяет обрабатывать матрицы данных как дихотомического (две категории), так и политомического типа (число категорий более двух). Использовали вид анализа Partial Credit Model [14]. Для расчета коэффициента альфа Кронбаха шкал опросника и проверки гипотезы о нормальности распределения латентных переменных с помощью критерия Колмогорова – Смирнова применяли пакет программ IBM SPSS 26. Для расчетов использовали также редактор электронных таблиц Excel 2016 и систему компьютерной алгебры Mathcad 15.0.

Пациенты с гистологически подтвержденным раком простаты (n = 100), которые находились под наблюдением в КДО ГКБ № 40 ДЗ г. Москвы с октября 2020 г. по декабрь 2021 г. и могли ответить на вопросы в анкетах
и ​​подписали формы информированного согласия, были приглашены принять участие в исследовании.

Основными жалобами пациентов были учащенное, ночью до трех – пяти раз, мочеиспускание, вялая струя и недержание мочи, иногда наличие цистостомического дренажа. Часть из них отмечали проблемы в половой сфере. Всем пациентам выполняли биопсию простаты, у большинства верифицирована ацинарная аденокарцинома простаты, выявлены фокусы PIN высокой степени и ASAP, доброкачественная гиперплазия предстательной железы, в дальнейшем этим пациентам была рекомендована повторная биопсия простаты.

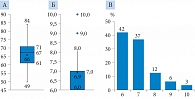
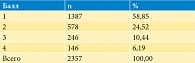
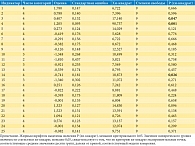
Возраст больных раком (табл. 2, рис. 2 А) варьировал от 49 до 84 лет (среднее значение – 66 лет, медиана – 67 лет, 1-й квартиль – 61, 3-й – 71 год, стандартное отклонение SD – 7,42, коэффициент вариации CV – 0,11). Таким образом, на первом месте в возрастной структуре заболевания были мужчины нетрудоспособного возраста.

Сумма баллов по Глисону больных (диапазон – 6–10, среднее значение – 6,90, медиана – 7,00, мода – 6, стандартное отклонение SD – 1,01, коэффициент вариации CV – 0,15) приведена в табл. 2 и на рис. 2 Б, В. Частота агрессивного рака по показателю Глисона (≥ 8) в наших наблюдениях составила 20,51%, что меньше, чем в психометрическом исследовании QLQ-PR25 [15] при опросе 633 больных РПЖ урологического отделения больницы Китайского медицинского университета (Тайвань) – 38,3%.

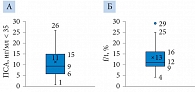
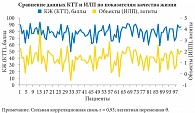
Большинство пациентов наблюдались урологом под контролем простатического специфического антигена (ПСА). Данные ПСА представлены в табл. 2 и на рис. 3. Уровень общего ПСА изменялся в весьма широких пределах (от 1,1 до 707 нг/мл), поэтому мы выполнили статистический анализ отдельно для всех пациентов и для пациентов, у которых ПСА менее 35 нг/мл (рис. 3 А). Во втором случае данные с ПСА > 35 нг/мл из корреляционного анализа исключали как попавшие под критерий точек выбросов. Среднее значение уровня ПСА больных составило 32,04 ± 90,29 нг/мл (M ± SD), что несколько отличается от данных [15] (46,3 ± 126,9 нг/мл до лечения, n = 135; 10,9 ± 33,5 нг/мл через месяц после лечения, n = 117; 2,8 ± 16,6 нг/мл через три месяца после лечения, n = 381). Авторы применяли хирургическое вмешательство, лучевую и гормональную терапию, химиотерапию.

Кроме того, анализировали соотношение общего и свободного ПСА – f/t (рис. 3 Б), важное для диагностики РПЖ (потерянные данные – 72%). Величина f/t изменялась от 4 до 29% со стандартным отклонением SD 6% и коэффициентом вариации CV 0,43. Среднее значение составило 13,21%, медиана – 11,87%.

Данные по стадиям рака пациентов были неполными, поэтому сравнение с результатами соответствующего анализа в работе [15] (I – 0,8; II – 67,2; III – 16,0; IV – 16,0%) не производилось.

Анализировали взаимные корреляционные связи между признаками: возраст, уровень концентрации в крови ПСА, отношение f/t, показатели по шкале Глисона больных. Установлена статистически значимая (p < 0,05) корреляционная связь средней силы (r = 0,53) между показателями ПСА и степенью злокачественности опухоли по Глисону. Между остальными переменными, включенными в исследование, парная корреляция была слабая или отсутствовала, что свидетельствует о том, что сопряженность рассмотренных признаков имеет сложный характер и требует дальнейших исследований.

Оценка опухоли по шкале Глисона – один из самых надежных инструментов, позволяющих врачу спрогнозировать, как поведет себя опухоль в ответ на лечение, насколько высок риск метастазирования или рецидива после хирургического удаления простаты [16]. С другой стороны, повышенный уровень ПСА диагностически ценен при наблюдении в динамике (однократное измерение малоинформативно). Тем не менее в данном исследовании опрос пациентов проводили на первичном приеме. Динамическую оценку ПСА и КЖ пациентов в различных точках процесса лечения больных не проводили.

Результаты и обсуждение

Классическая теория тестирования

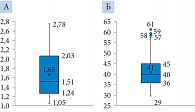
Описательная статистика. Статистический анализ включал данные описательной статистики и оценку статистической значимости различий. “Box and whiskers” среднего исходного («сырого») балла больных при опросе представлен на рис. 4 А. При теоретически минимальном значении 0 и максимальном 4 наименьшее значение среднего балла по пунктам составило 1,05, наибольшее – 2,78, среднее значение – 1,65, медиана – 1,51, стандартное отклонение – 0,54, коэффициент вариации – 0,33.

Эти же данные по шкалам составили: шкала 1 – симптомы мочевыделительной системы (среднее значение – 1,82, медиана – 1,72, стандартное отклонение SD – 0,62, коэффициент вариации CV – 0,33), шкала 2 – симптомы патологии кишечника (среднее значение – 1,17, медиана – 1,12, стандартное отклонение SD – 0,15, коэффициент вариации CV – 0,13), шкала 3 – гормональные симптомы, связанные с заболеванием (среднее значение – 1,33, медиана – 1,26, стандартное отклонение SD – 0,21, коэффициент вариации CV – 0,15), шкала 4 – способность к репродукции (сексуальная активность и сексуальная функция) (среднее значение – 2,01, медиана – 2,03, стандартное отклонение SD – 0,54, коэффициент вариации CV – 0,33).

Наименьшее значение суммы приведенных баллов при теоретически минимальном значении 0 и максимальном 100 составило 29, а наибольшее – 61 при среднем значении 40,6 и медиане 40 (рис. 4 Б).

Представляет интерес структура ответов респондентов (табл. 3).

«Совсем нет» чаще всего (в 90% случаев) респонденты ответили на вопросы PR12 «Наблюдали ли Вы кровь в стуле?» и PR15 «Испытывали ли Вы боль в груди и сосках, было ли их увеличение?» (PR15). «Очень часто» чаще всего (40%) отвечали на вопрос PR4 «Не высыпаетесь ли Вы ночью из-за необходимости часто вставать в туалет?». «Совсем нет» реже всего (3%) респонденты дали ответ на вопрос PR1 «Как часто Вы мочились в течение дня?». «Очень часто» реже всего (0%) пациенты отвечали на вопросы PR10–12 и PR15.

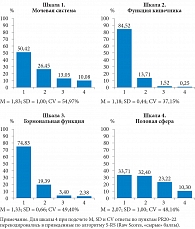
Структура вариантов ответов респондентов по отдельным функциональным шкалам (симптоматическим субшкалам) приведена на рис. 5 (по оси абсцисс – варианты ответов).

Со структурой балльных показателей тесно связана такая характеристика, как распространенность симптомов (prevalence). Наше исследование показало, что у больных РПЖ наиболее распространены симптомы мочевыделительной системы – 49,58%, реже встречаются симптомы снижения сексуальной активности и функции – 31,39%, еще реже (25,17%) – гормональные симптомы, связанные с заболеванием, и очень редко (15,48%) – симптомы патологии кишечника, что вполне объяснимо для больных раком предстательной железы. Средняя распространенность всей рассмотренной симптоматики составила 33,69%. Наиболее распространенным и часто встречающимся (96,91%) оказался симптом, связанный с ответами на вопрос PR1 «Как часто Вы мочились в течение дня?», а наиболее редким (5,15%) – обусловленный недержанием стула PR11 (шкала «Симптомы патологии кишечника»).

Интегральный уровень КЖ пациентов составил 79,46% (рис. 6), что несколько выше, чем в исследовании В.И. Широкорада и соавт., обследовавших 236 больных РПЖ при помощи опросника EORTC QLQ-C30 (56%, диапазон 40–80%) [17], и практически не отличается от данных [18]. Таким образом, выявлен весьма высокий уровень жизни больных, который соответствует известным данным о том, что, хотя рак простаты и занимает четвертое место по распространенности, он не входит в список онкологических заболеваний с наиболее низким КЖ и высоким риском смертности (особенно на ранних стадиях заболевания) [4].

Не на все вопросы анкеты были даны ответы. Потерянные данные (missing data) по шкалам составили 6,33; 1,50; 2,00 и 11,33%. Общий процент недостающих данных составил 5,72 (143 ячейки из 2500 матрицы данных). Наиболее трудными (вопросы, на которые больные не смогли ответить) были вопросы домена «Снижение сексуальной активности и функции» (PR20–25), почти у всех респондентов не возникло проблем при ответе на вопросы сферы «Патология кишечника» (PR10–13). Однако нужно отметить, что на вопросы PR22–25 «В какой степени секс был приятен Вам?», «Были ли у Вас трудности с достижением и поддержанием эрекции?», «Были ли у Вас проблемы с семяизвержением (например, сухое семяизвержение)?», «Чувствовали ли Вы себя некомфортно во время сексуальной близости?» отвечали только больные, которые были сексуально активны в течение последних четырех недель. Также заметим, что самым трудным вопросом опросника оказался вопрос шкалы 1 (симптомы мочевыделительной системы) «Недержание мочи является для Вас проблемой?» – на него не ответили 28% больных.

В качестве психометрических свойств опросника EORTC QLQ-PR25 изучали самосогласованность (альфа Кронбаха), успешность шкалирования и совместимость заданий.

Согласованность данных, полученных при тестировании больных (среди них были люди пожилого и старческого возраста – 76%), проверяли с помощью расчета величины альфа Кронбаха. Диапазон изменения коэффициента – от 0 до 1. Как известно, это один из эффективных критериев однородности состава заданий, качества и валидности теста. По сути, он оценивает разброс ответов на каждый вопрос с общим разбросом ответов всей шкалы или теста и может быть произведен по формуле

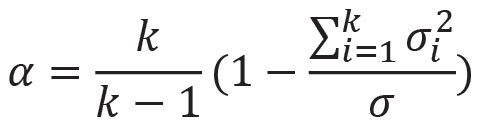 , (2)

  где α – коэффициент Кронбаха; k – количество пунктов (заданий) теста (25);  – дисперсия по i-му пункту теста;  – дисперсия суммарных баллов по всему тесту.

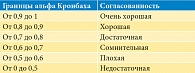
Возможные значения коэффициента альфа Кронбаха и общепринятая интерпретация приведены в табл. 4 [19].

Расчет проводили с помощью приложений статистического пакета IBM SPSS Statistics 26 (StatSoft Inc, США) и редактора таблиц Microsoft Excel 2016 (Microsoft, США).

Результаты расчета альфа Кронбаха в среде Excel 2016 – 0,861; SPSS 26 – 0,766. Средняя внутренняя согласованность ответов на пункты опросника EORTC QLQ-PR25 (n = 100) составила 0,814, что, согласно табл. 4, соответствует хорошей.

По шкалам в отдельности (табл. 5) согласованность данных (SPSS) составила: симптомы мочевыделительной системы (PR1–9) – 0,749; симптомы патологии кишечника (PR10–13) – 0,423; гормональные симптомы, связанные с заболеванием (PR14–19), – 0,513; способность к репродукции (сексуальная активность и сексуальная функция, PR20–25) – 0,704, что несколько неожиданно, но коррелирует с данными [12], полученными в отделении урологии Национальной больницы Тайваньского университета на основании тайваньско-китайской версии EORTC QLQ-C30 (версия 3.0) и EORTC QLQ-PR25 при обследовании 81 больного раком простаты I–IV стадий, – 0,80; 0,41; 0,45; 0,64 соответственно.

Корреляция между пунктами шкал. Также на основании матрицы корреляции изучали диапазон корреляции между пунктами опросника (пунктами внутри одной шкалы и пунктами внутри разных шкал) (табл. 5). Наименьший показатель связи между вопросами одной шкалы (0,0005) зарегистрирован между пунктами PR4 «Не высыпаетесь ли Вы ночью из-за необходимости часто вставать в туалет?» и PR9 «Ваша повседневная (ежедневная) активность ограничивается урологическими проблемами?», наибольший (0,67) – между PR8 «Ответьте на этот вопрос, только если у Вас есть недержание: недержание мочи является для Вас проблемой?» и PR9. Самая слабая корреляционная связь между пунктами различных шкал (0,002) была у ответов на вопросы PR9 и PR20 «Насколько Вы заинтересованы в сексе?» (шкалы 1 и 4), самая сильная (0,48) – у ответов на вопросы PR13 «Было ли у Вас вздутие живота?» и PR19 «Чувствовали ли Вы себя менее мужественным в результате ваших недугов или лечения?» (шкалы 2 и 3).

Успешность шкалирования. Мы не встречали в отечественной литературе перевода на русский язык термина “scaling success”. Дословный перевод означает успешность шкалирования. В [20] предлагается определять его как конвергентную валидность. Аналогичную интерпретацию дают авторы [21]. Смысл фактора состоит в том, насколько сила связей между элементами определенных симптоматических шкал больше, чем сила связи этих элементов с компонентами других шкал, нацеленных на измерение другой симптоматики. Характеризует не только связи проверяемого теста с близкородственными показателями, но и те, где значимых связей наблюдаться не должно. Установлена успешность шкалирования, равная 100%, для всех четырех доменов EORTC QLQ-PR25 (табл. 5), что существенно выше, чем в исследовании [12] (15/27, 1/12, 4/18 и 6/6 соответственно). То есть взаимная корреляция между любым пунктом любой шкалы опросника и суммой пунктов этой шкалы выше, чем сила корреляции между этим пунктом и суммой пунктов любой другой шкалы (всего было исследовано 25 × 4 = 100 корреляционных связей). Таким образом, данный психометрический инструмент является менее чувствительным, чем мониторинг силы корреляции между отдельными пунктами функциональных шкал опросника на основании вычисления матрицы корреляции.

Совместимость. Совместимость заданий обозначает силу связи каждого пункта с итоговым показателем и рассчитывается как коэффициент корреляции пункта с итоговым показателем. Чем выше значение коэффициента, тем лучше пункт «вписывается» в определенную или итоговую шкалу. Минимальное допустимое значение принято равным 0,2. В противном случае делается вывод, что этот пункт измеряет какое-то другое свойство, не имеющее отношения к разрабатываемой шкале или тесту [22]. Когда значение коэффициента совместимости приближается к нулю или отрицательно, проверяемый пункт теста должен быть пересмотрен в связи с некорректностью формулировки задания или вариантов ответа на него. В нашем случае это может означать, что пациенты с большим балльным показателем КЖ имеют высокую симптоматику по данному пункту и, наоборот, больные с низким КЖ – отсутствие данных симптомов. Этому критерию, согласно табл. 4, удовлетворяют пункты PR12 «Наблюдали ли Вы кровь в стуле?» и PR15 «Испытывали ли Вы боль в груди и сосках, было ли их увеличение?» (совместимость 0,15 и 0,19), и их присутствие в наборе вопросов опросника в данной формулировке требует дополнительного изучения. Кстати отметим, что из всех 25 вопросов опросника на эти вопросы респонденты отвечали чаще всего «Совсем нет» (90%) и реже всего «Очень часто» (0%). В целом совместимость заданий опросника EORTC QLQ-PR25 составила 0,31.

Теория измерения латентных переменных (анализ данных с помощью диалоговой системы ИЛП)

Параметрами модели Раша являются латентные переменные θ (характеристика измерения объектов) и β (характеристика измерения индикаторов). Результат их взаимодействия в модели описывается логистической функцией

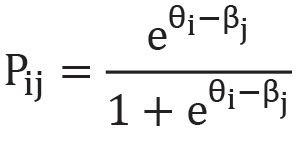 , (3)

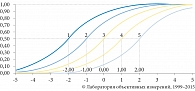
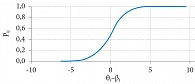
где P_ij – вероятность ослабления ниже определенного уровня или полного подавления у i-го пациента j-го симптома. В отличие от классической теории тестирования, оперирующей с эмпирическим массивом данных в виде матрицы, в теории латентных переменных величины θ и β измеряются на одной и той же шкале – шкале логитов, которая является линейной (рис. 7). Таким образом, логит – это мера измерения латентной величины по шкале натуральных логарифмов, а разность аргументов логит-функции просто отображает проекцию шансов события P_ij/1-P_ij на промежуток реальных чисел в результате логарифмирования.

В самой общей формулировке P_ij означает вероятность успеха у i-го объекта по j-му индикатору. Она варьирует следующим образом (табл. 6).

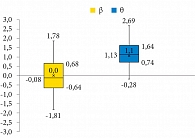
Интерпретация латентных переменных. Как уже отмечалось, в статистике под латентными или скрытыми переменными понимают такие переменные, которые не могут быть измерены в явном виде, а могут быть только выведены через математические модели с использованием наблюдаемых переменных. Мы считаем, что если рассматривать P_ij как вероятность ослабления и подавления у i-го больного некоторого j-го симптома, то переменная θ_i может означать реактивность, уровень здоровья, «внутренние резервы» организма i-го пациента, его адаптационно-компенсаторные возможности до лечения и эффективность терапевтического или иного лечебного воздействия в результате лечения, а β_j – болезнетворный потенциал латентных патогенных факторов, вызывающих/влияющих на появление и развитие j-го симптома. В результате чем больше θ i-го пациента и чем меньше β соответствующего j-го фактора, тем больше вероятность P_ij ослабления и подавления соответствующего симптома, и наоборот, чем меньше θ i-го пациента и чем больше β соответствующего j-го фактора, тем меньше вероятность P_ij ослабления и подавления этого симптома, что полностью соответствует ходу кривой на рис. 7 и данным табл. 6. Предложенная интерпретация латентных переменных согласуется с концепцией силового поля К. Левина [23] в рамках психологической теории. С этой точки зрения (баланса двух противоположно направленных систем сил) латентную переменную β обусловливает мера патогенности потенциально болезнетворных стимулов, а переменная θ хорошо сочетается с защитными возможностями организма (до лечения) вкупе с эффективностью терапевтического или другого лечебного воздействия (после лечения и реабилитации) (рис. 8).

Для получения численных оценок латентных переменных в модели Раша необходимо приблизить теоретические вероятности P_ij к приведенным эмпирическим оценкам частот проявления соответствующих симптомов, полученным с помощью опросника при сборе информации. Это и реализует диалоговая система ИЛП.

Общие статистики. В результате счета система возвращает следующие группы показателей: индикаторы, объекты, характеристики измерительного инструмента, показатели надежности. Здесь и в дальнейшем используется терминология, принятая в современной теории тестирования. Под индикаторами понимаются пункты опросника, под объектами – пациенты. Здесь и далее мы сочли возможным не отступать от сложившейся терминологии, за исключением названий латентных переменных: θ_i – уровень подготовленности i-го испытуемого, β_j – трудность j-го задания, P_ij – вероятность правильного ответа i-го испытуемого на j-й вопрос (общепринятых в педагогических измерениях и системах оценивания) [7].

Результаты описательной статистики КЖ 100 больных РПЖ даны в следующем виде.

Индикаторы: среднее значение (логит) – 0,000, ошибка измерения (логит) – 0,916.

Объекты: среднее значение (логит) – 1,166, ошибка измерения (логит) – 0,623.

Характеристики измерительного инструмента: число индикаторов – 25, число объектов – 100, число подгрупп объектов – 10, статистика хи-квадрат – 347,022, число степеней свободы – 225.

Показатели надежности: индекс сепарабельности объектов (близкий по смыслу к коэффициенту альфа Кронбаха) – 0,706; альфу Кронбаха не вычисляли, поскольку в матрице исходных данных были пропущенные данные.

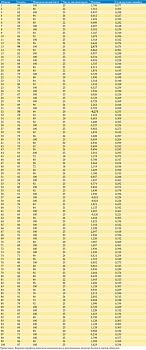
Индикаторы. В табл. 7 приведены результаты расчета индикаторов опросника EORTC QLQ-PR25. Как следует из результатов, число категорий на вопросы варьирует от 2 до 4, оценка – от -1,81 до 1,78 логит, средняя оценка – 0 логит, стандартная ошибка – от 0,09 до 0,44 логит, статистика хи-квадрат – от 5,62 до 98,74, число степеней свободы – 9.

Наименьшая оценка из набора индикаторов соответствует индикатору 11 «Случалось ли у Вас недержание стула?» с наименьшим первичным балльным показателем 1,05 и КЖ по этому показателю 95,75%. Наибольшая оценка – ожидаемо индикатору 1 «Как часто Вы мочились в течение дня?» с наибольшим первичным балльным показателем 2,73 и КЖ по этому показателю 55,00%.

Критерий согласия хи-квадрат у большинства индикаторов больше 0,05 (за исключением 3-го «Торопитесь ли Вы в туалет, когда чувствуете нужду помочиться?», P (хи-квадрат) = 0,04, 4-го «Не высыпаетесь ли Вы ночью из-за необходимости часто вставать в туалет?», P (хи-квадрат) = 0,00, и 14-го «Вас бросало в жар?», P (хи-квадрат) = 0,02). Вне сомнения, эти значения показателей считаются более чем удовлетворительными и свидетельствуют о высокой точности выполненной параметризации. Это означает, что полученные результаты опроса пациентов с помощью представленного в опроснике состава пунктов можно использовать как для измерения рассматриваемой латентной переменной, так и для измерения уровня КЖ. При этом в отношении 3, 4 и 14-го индикаторов, не адекватных модели измерения, необходимы дополнительные исследования. Пока только можем отметить, что статистика хи-квадрат у данных индикаторов максимальная (17,14; 98,73 и 18,87 соответственно), а разброс балльных показателей по четвертому индикатору больше, чем у других индикаторов (стандартное отклонение 1,25).

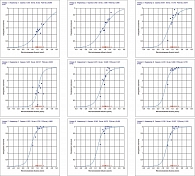
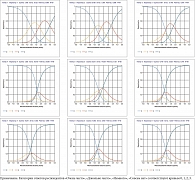
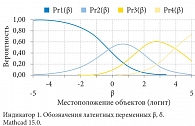
Характеристические кривые. В рамках теории латентных переменных индикаторная переменная полностью определяется ее характеристической кривой. Характеристические кривые индикаторов представлены на рис. 9. Графики с характеристическими кривыми имеют следующую структуру. На оси абсцисс показаны значения латентной переменной, в данном случае это «местоположение объекта» (θ). Эта латентная переменная, как и любые другие латентные переменные в рамках теории латентных перемен, измеряется в логитах. На оси ординат показаны значения рассматриваемого индикатора. В диалоговой системе ИЛП значение любого индикатора начинается с нуля.

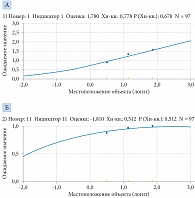
Для наглядности представлен подробный анализ наиболее отличительных индикаторов. Из всего набора акцент сделан на двух вопросах (1 и 11): «Как часто Вы мочились в течение дня?» и «Случалось ли у Вас недержание стула?» с распространенностью симптома 96,91 и 5,15% (это самые высокие и низкие значения распространенности симптома среди всех индикаторов). Кроме того, согласно табл. 7, первому индикатору соответствует самая высокая оценка – 1,78, а 11-му – самая низкая – -1,81 логит. Соответствующие характеристические кривые индикаторов (в представлении число подгрупп объектов 3) даны на рис. 10.

Характеристическая кривая на рис. 10 А имеет наибольшую крутизну в правой части шалы. Это означает, что индикатор 1 лучше, чем остальные, дифференцирует пациентов с высоким КЖ. Наибольшая крутизна кривой на рис. 10 Б находится в левой части шкалы. Это означает, что эта кривая лучше других дифференцирует больных с низким КЖ.

Заметим также, что индикатор 4 («Не высыпаетесь ли Вы ночью из-за необходимости часто вставать в туалет?») плохо соответствует модели измерения Раша, поскольку ответы обследуемых противоречат логическому основанию модели (рис. 9, диаграмма 4).

Кривые распределения категорий. Кривые распределения категорий (в англоязычной литературе – Item Characteristic Curve, ICC) определяют вероятность достижения случайной политомической величины x_ni значения x в семействе моделей Раша:

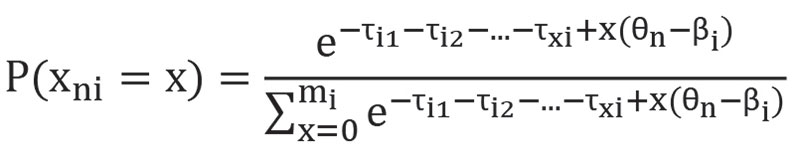 , (4)

где латентные переменные обозначены символами θ_n и β_i; m_i – число категорий i-го индикатора; τ_xi – пороги индикаторных переменных.

В случае политомической переменной x_ni = 0, 1, 2, 3 уравнение (4) распадается на четыре:

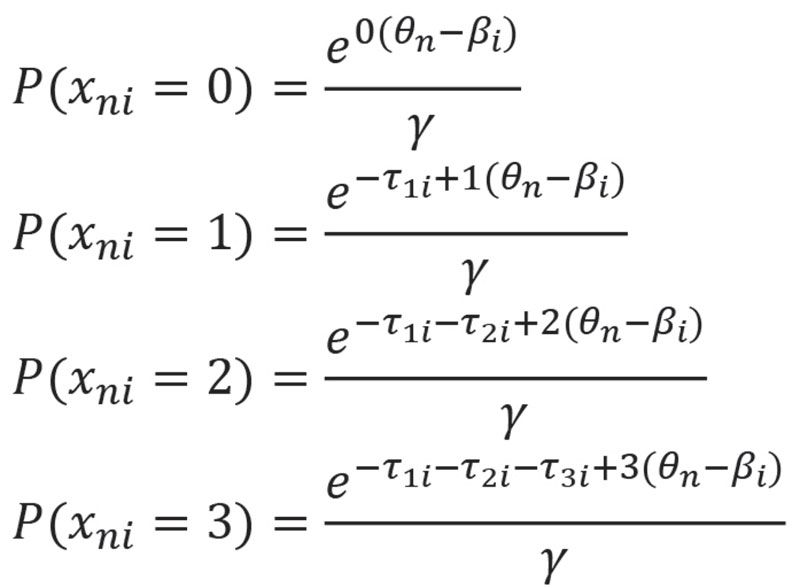 , (5)

 где

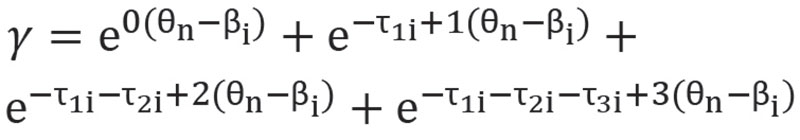, (6)

Здесь P(x_ni = 0) + P(x_ni = 1) + P(x_ni = 2) + P(x_ni = 3) = 1.

Кривые распределения категорий ответов при опросе больных РПЖ приведены на рис. 11.

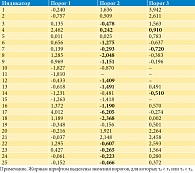
Пороги кривых распределения категорий. Пороги отделяют категории индикатора друг от друга. Как известно, это точка на шкале латентной переменной, в которой вероятность выбора соседних категорий совпадает. Например, у 1-го индикатора порог 1 равен -0,240 логит, в этой точке пересекаются кривые категорий 0 и 1, порог 2 равен 1,636 логит, в этой точке пересекаются кривые категорий 1 и 2 и т.д. На рисунке видно, как и на каком интервале шкалы латентной переменной работает каждая категория. Например, нулевая категория описывает вероятность того, что пациенты с уровнем латентной переменной θ очень часто «мочились в течение дня», и при θ < -0,240 логит эта категория ответов опросника наиболее вероятна. В интервале -0,240 < θ < 1,636 логит вероятнее всего категория 1, соответствующая ответу пациентов довольно часто «мочились в течение дня», и т.д. (табл. 8). Таким образом, наименьшие значения латентной переменной θ (в логитах) соответствуют высокой эвентуальности ответов опросника в категории «0 баллов», что на основании матрицы ответов респондентов означает низкий уровень КЖ, и наоборот, большие значения этой переменной отвечают высокой вероятности категории в 4 балла и, соответственно, отменному на основании матрицы данных КЖ пациента, что согласуется с логическим основанием модели Раша.

Отметим, что в дихотомическом случае для индикатора 11 (отсутствуют категории ответов «Очень часто», «Довольно часто») кривые распределения категорий представлены только двумя кривыми и, соответственно, одним пороговым значением -1,810 логит.

Для индикатора 1 все категории использовались исследователями для оценки КЖ. «Неработоспособных» категорий индикатора нет. Все категории имеют свой интервал измерения, где они работают, а пороги τ₁ < τ₂ < τ₃. Однако для индикатора 3 не все пороги расположены в порядке возрастания. В частности, нет области континуума θ, в которой оценка 1 («Довольно часто») является наиболее вероятной. То есть в области ответов на вопросы опросника, где ожидаемый (средний) балл равен 1, пациенты с большей вероятностью дадут балл из другой категории. По мере увеличения интегрального показателя КЖ вероятность получения более высокого балла по данному индикатору монотонно не увеличивается, а балл 1 никогда не бывает наиболее вероятным. Это означает, что данный пункт опросника следует изучить дополнительно, чтобы понять, почему категория работает не так, как ожидалось на основании модели Раша. Это может быть связано с недостаточным объемом выборки, кроме того, P (хи-квадрат) для третьего индикатора 0,047, а это говорит о том, что элемент не соответствует модели. При этом характеристическая кривая индикатора 3 по отношению к групповым средним имеет приемлемый вид (рис. 9, диаграмма 3). Аналогичные ситуации наблюдались для ряда других индикаторов.

Таким образом, диагностический модуль EORTC QLQ-PR25 имеет весьма высокие показатели валидности по отношению к модели измерения Раша и позволяет объективно оценивать КЖ на первичном приеме онкоурологических больных, но, возможно, нуждается в доработке набора индикаторов или увеличении числа тестируемых.

Оценки объектов. В опросе о КЖ приняли участие 100 пациентов. Результаты оценки объектов представлены в табл. 9. Среднее значение оценки объектов – 1,16. Сумма первичных баллов пациентов варьировала от 50 (минимальный уровень КЖ), ей соответствовала минимальная оценка -0,275 логит (больной В., 69 лет, ПСА – 20,5 нг/мл, показатель по Глисону – 8), до 94 (максимальный уровень КЖ) – максимальная оценка 2,475 логит (больной М., 60 лет, ПСА – 72,7 нг/мл, показатель по Глисону – 9), число индикаторов – от 18 до 25. Средняя стандартная ошибка – 0,33, коэффициент вариации стандартной ошибки – 0,21. Пропуск данных для некоторых комбинаций (обследуемый/индикаторная переменная) не является критическим [24].

Зарегистрированная агрессивная степень рака у больного с высоким уровнем КЖ соответствует низкому установленному коэффициенту корреляции r (сумма по Глисону; КЖ) = -0,09, что, на наш взгляд, можно интерпретировать как ложное снижение степени корреляции вследствие гетерогенности данных, вызванной принадлежностью обследованных к разным категориям индивидуумов (парадокс Симпсона) [25]. Вследствие этого мы провели дополнительное исследование силы связи между суммой баллов по Глисону и КЖ больных для средних значений диапазонов данных и в результате получили коэффициент корреляции r (сумма по Глисону; КЖ) = -0,54, что по шкале Чеддока означает обратную связь средней силы. Аспекты неоднородности обследованных пациентов в рамках Differential Item Functioning (DIF) [15] не изучали.

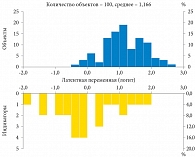
Местоположение латентных переменных. Одной из задач модели является установка взаимосвязи между двумя множествами θ_i и β_j и распределения их значений на единой линейной шкале логит (рис. 12, 13). На рисунке 12 на верхней диаграмме показано частотное распределение латентной переменной θ_i, на нижней – индикаторной переменной β_j на одной линейной шкале логит и результат взаимодействия между этими множествами. Для удобства в качестве точки отсчета (нуля) рассматривают среднее значение β_j.

Знание средних значений переменных по объектам и индикаторам (θ и β) позволяет оценить среднюю вероятность «успеха» P в модели Раша, которая может быть вычислена по формуле (1) для логистической функции и интерпретирована как уровень КЖ пациентов. Она оказывается равной 76,24%, что несколько меньше, чем индекс КЖ, рассчитанный в КТТ, – 79,46%. В то же время при использовании всего спектра значений множества латентных переменных для расчета значений соответствующих вероятностей, а затем их усреднения получаем значение КЖ ИЛП – 73,03%. Возможно, эти различия связаны с тем, что баллы в классическом методе подсчета КЖ находятся на интервальной, а не на линейной шкале, как латентные переменные в современной теории. В любом случае феномен требует дальнейшего анализа и рассмотрения на предмет точности моделей измерения КЖ, интерпретации и идентичности даваемых ими результатов.

Анализ гистограмм на рис. 12 позволяет заключить, что распределение переменных θ и β близко к нормальному: относительно небольшое число пациентов с низким и высоким уровнями резервов организма и относительно большое число пациентов со средней резистентностью к заболеванию (θ). Те же самые показатели справедливы и для характеристики кривой для симптомокомплекса (β). Действительно, количественная проверка гипотезы о нормальности с помощью одновыборочного критерия Колмогорова – Смирнова дает результат, что проверяемые распределения являются нормальными (статистика критерия 0,066 для переменной θ и 0,116 для переменной β, двусторонняя асимптотическая значимость 0,200 с коррекцией значимости Лильефорса). Напомним, что если статистика Колмогорова – Смирнова значима (p < 0,05), то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.

Для признания теоретических значений параметров модели в качестве точных необходимо дать оценку соответствия опытных данных модели.

Сравнение показателей КЖ согласно классической теории тестирования и теории латентных переменных (диалоговой системы ИЛП). Метрическая модель Раша является общепризнанной теорией перехода от индикаторных переменных к латентным. Результат такого преобразования можно оценить путем изучения корреляции между данными. Взаимная корреляционная связь между балльными показателями КЖ, рассчитанными согласно КТТ, и латентными переменными θ и β, определяющими КЖ согласно модели измерения Раша, оказалась исключительно сильной – 0,93 и -0,97 соответственно. О сильной корреляции результатов измерений свидетельствуют графики, представленные на рис. 14 и 15. На основании этих данных следует, что с определенной точностью латентную переменную θ можно принимать за уровень КЖ, рассчитанный по выборке больных (рис. 14). Статистическая взаимосвязь, установленная между интегральным уровнем КЖ и величиной индикаторной переменной β, является обратной (отрицательной) (рис. 15), но весьма значительной, вследствие чего эту латентную переменную также можно принять за один из показателей КЖ больных. Показатель взаимной корреляции, рассчитанный между модельными вероятностями, определенными по формуле (3) для логистической функции, и балльными показателями КЖ, оказался равным 0,95.

Матрицы оценок и вероятностей. От приложения RUMM диалоговая система ИЛП отличается опцией построения матриц оценок и вероятностей ответов. Матрицы строятся на основании оценок объектов и индикаторных переменных.

В матрице оценок ответов (табл. 10) пациентов выделены первая строка, содержащая оценки местоположения индикаторов, и первый столбец с оценками местоположения объектов. Элемент матрицы A_ij вычисляется следующим образом:

 A_ij = 0 ∙ P(θ_i, β_j, 0) + 1 ∙ P(θ_i, β_j, 1) + 2 ∙ P(θ_i, β_j, 2) + 3 ∙ P(θ_i, β_j, 3), (7)

 где P(θ_i, β_j, k) – вероятность i-го объекта выбрать категорию k в j-м индикаторе.

В качестве примера рассчитано значение первой ячейки матрицы i = 1, j = 1, θ₁ = 1,79, β₁ = 1,78, приведенные значения порогов τ₁ = -2,08223 - β₁, τ₂ = -0,64993 - β₁, τ₃ = 0,477723 - β₁. По формуле (6) определили γ = 18,521, по формулам (5) – P(θ₁, β₁, 0) = 0,053, P(θ₁, β₁, 1) = 0,411, P(θ₁, β₁, 2) = 0,479, P(θ₁, β₁, 3) = 0,055. Отсюда на основании (7) A₁₁ = 1,537, что соответствует значению A₁₁ = 1,54 в табл. 10. Расчеты проводили в среде компьютерной алгебры Mathcad 15.0.

В матрице оценок цвет ячейки определяет соответствие фактических значений в исходной матрице первичных («сырых») данных и ожидаемых в результате расчета категорий (рис. 16). Это позволяет определить, насколько исходные данные отличаются от модели измерений.

Матрица вероятностей ответов представлена в табл. 11. В данном случае элементом матрицы является вероятность P(θ_i, β_j, k), где k – категория, фактически выбранная объектом i в j-й индикаторной переменной. Например, в ячейке A₁₁ в табл. 10 (категория 2) P(θ₁, β₁, 2) = 0,479, что соответствует значению 0,48 в табл. 11. Цвет ячеек в таблице соответствует определенному значению вероятности (рис. 17).

Выполненные в этом разделе расчеты позволили произвести проверку правильности построения кривых распределения категорий (рис. 11) путем построения этих кривых в системе компьютерной алгебры Mathcad 15.0 на примере первого индикатора (рис. 18) и вычисления порогов кривых: τ₁ = -0,240, τ₂ = 1,636, τ₃ = 3,942 логит.

Результаты проверки показали высокую точность работы диалоговой системы ИЛП, использованной для обработки данных тестирования.

Выводы

Исследовано качество жизни 100 пациентов онкоурологического профиля, находившихся под наблюдением в КДО ГКБ № 40 ДЗ г. Москвы с октября 2020 г. по декабрь 2021 г. Установлена статистически значимая корреляционная связь средней силы (r = 0,53) между показателями ПСА и степенью злокачественности опухоли (по Глисону). Для математической обработки данных опросника КЖ EORTC QLQ-PR25 применяли классическую (КТТ) и современную теорию тестирования на основе диалоговой системы ИЛП.

Коэффициент альфа Кронбаха данных составил 0,81, самосогласованность по функциональным шкалам: симптомы мочевыделительной системы – 0,749; симптомы патологии кишечника – 0,423; гормональные симптомы, связанные с заболеванием, – 0,513; способность к репродукции (сексуальная активность и сексуальная функция) – 0,704. Совместимость заданий опросника равна 0,31, успешность шкалирования (scaling success) – 100%.

Распространенность симптомов по рассмотренным шкалам соответствовала 49,58; 15,48; 25,17 и 31,39%, выраженность – 27,47; 5,79; 11,15 и 37,76%. Интегральный уровень КЖ больных РПЖ составил 79,46 (КТТ) и 76,24% (ИЛП).

С помощью системы ИЛП получена детальная описательная статистика результатов испытаний, выполнено исследование индикаторов (оценок, стандартного отклонения SD, статистики хи-квадрат, P (хи-квадрат), характеристических кривых, кривых распределения категорий и их порогов), соответствия экспериментальных данных теоретической модели, а также объектов (баллов, оценок, стандартной ошибки среднего SEM), местоположения индикаторов и объектов и их распределения. В качестве инструмента для объективного измерения латентных параметров применяли признанную в мировом научном сообществе метрическую модель Раша. Средняя оценка объектов θ установлена равной 1,166 при средней оценке индикаторов β 0 логит. Вычислены матрицы оценок ответов в представлении «оценки» и «вероятности».

На основании одновыборочного критерия Колмо­горова – Смирнова подтверждена гипотеза о нормальности распределения латентных переменных (статистика критерия 0,066 для переменной θ и 0,116 для переменной β).

Сопоставлены первичные балльные оценки КЖ пациентов, полученные классическим аддитивным методом суммирования первичных баллов по пунктам (пациентам) опросника, и показатели, рассчитанные на основании теории латентных переменных. Коэффициент корреляции Пирсона составил 0,93 (-0,97). Показатель корреляции, рассчитанный между модельными вероятностями, определенными по формуле для логистической функции, и балльными показателями КЖ, – 0,95.

Впервые предложена интерпретация латентных переменных в медицине на основании концепции силового поля К. Левина. Качество жизни больных следует рассматривать как динамический баланс двух противоположно направленных систем сил, при этом латентная переменная β определяет влияние негативных патогенных факторов на субъективную оценку самочувствия больного, переменная θ – защитные адаптационно-компенсаторные возможности организма до лечения и эффективность терапевтического или другого лечебного воздействия после лечения и реабилитации.